题目内容
设关于x的函数y=2cos2x-2acosx-（2a+1）的最小值为f（a），试确定满足
的a的值，并对此时的a值求y的最大值．
解：令cosx=t，t∈[-1，1]，
则y=2t2-2at-（2a+1），对称轴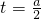
，
当
，即a＜-2时，[-1，1]是函数y的递增区间，
；
当
，即a＞2时，[-1，1]是函数y的递减区间，
，
得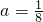
，与a＞2矛盾；
当
，即-2≤a≤2时，
得a=-1，或a=-3，
∴a=-1，
此时ymax=-4a+1=5．
分析：先令cosx=t，转化为关于t的一元二次函数；通过讨论对称轴和去件的位置关系找到最小值f（a）；再结合即可求出a的值并求出y的最大值．
点评：本题主要考查二次函数在闭区间上的最值讨论问题．解决问题的关键在于讨论对称轴和区间的位置关系．
则y=2t2-2at-（2a+1），对称轴
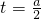，当
，即a＜-2时，[-1，1]是函数y的递增区间，；当
，即a＞2时，[-1，1]是函数y的递减区间，，得
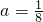，与a＞2矛盾；当
，即-2≤a≤2时，得a=-1，或a=-3，
∴a=-1，
此时ymax=-4a+1=5．
分析：先令cosx=t，转化为关于t的一元二次函数；通过讨论对称轴和去件的位置关系找到最小值f（a）；再结合
即可求出a的值并求出y的最大值．点评：本题主要考查二次函数在闭区间上的最值讨论问题．解决问题的关键在于讨论对称轴和区间的位置关系．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
的a的值，并求此时函数y的最大值．