题目内容

精英家教网若函数y=Asin（ωx+φ），（A＞0，ω＞0，|φ|＜
π
2
在一个周期内的图象如图所示，M，N分别是这段图象的最高点和最低点，且
OM
•
ON
（O为坐标原点），则A•ω=（　　）
A、
π
6
B、
7
12
π
C、
7
6
π
D、
7
3
π
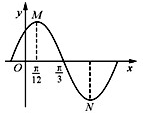
分析：根据图象求出函数的周期，再求出ω的值，根据周期设出M和N的坐标，利用向量的坐标运算求出A的值．
解答：解：由图得，T=4×(
π
3
-
π
12
)=π，则?=2，
设M（
π
12
，A），则N（
7π
12
，-A），
∵
OM
•
ON
=0，A＞0，∴
π
12
×
7π
12
-A×A=0，解得A=
7π
12
，
故选B．
点评：本题考查了由函数图象求出函数解析式的方法，考查向量的数量积的计算，考查了读图能力．
练习册系列答案
相关题目
若函数y=Asin（ωx+φ）（ω＞0）与x轴的两个相邻的交点坐标为（-4，0），（2，0），则ω=
 
．
（2012•吉林二模）若函数y=Asin（ωx+φ）+b（A＞0，ω＞0，|φ|＜
π
2
）在一个周期内的图象如图所示，则函数的解析式为（　　）
（2012•蚌埠模拟）若函数y=Asin(ωx+φ)(A＞0，ω＞0，|φ|＜
π
2
)在一个周期内的图象如图所示，M，N分别是这段图象的最高点和最低点，O为坐标原点，且
OM
•
ON
=0，则A•ω=
7
π
6
7
π
6
．
若函数y=Asin（ωx+φ）+m的最大值为4，最小值为0，最小正周期为
π
2
，直线x=
π
3
是其图象的一条对称轴，则它的解析式是（　　）
A、y=4sin（4x+
π
6
）
B、y=2sin（2x+
π
3
）
C、y=2sin（4x+
π
3
）
D、y=2sin（4x+
π
6
）+2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网