题目内容
设 ,
, .
.
(1)当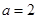 时,求曲线
时,求曲线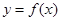 在
在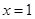 处的切线方程;
处的切线方程;
(2)如果存在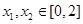 ,使得
,使得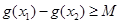 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数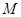 ;
;
(3)如果对任意的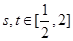 ,都有
,都有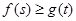 成立,求实数
成立,求实数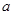 的取值范围
的取值范围
 ,
, .
.(1)当
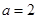 时,求曲线
时,求曲线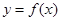 在
在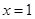 处的切线方程;
处的切线方程;(2)如果存在
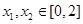 ,使得
,使得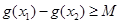 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数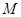 ;
;(3)如果对任意的
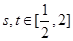 ,都有
,都有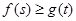 成立,求实数
成立,求实数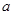 的取值范围
的取值范围(1)当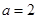 时,
时,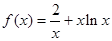 ,
, ,
, ,
, ,
,
所以曲线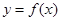 在
在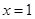 处的切线方程为
处的切线方程为 .
.  (3分)
(3分)

考察 ,
,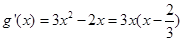 ,
,
由上表可知: ,
,
 ,
,
所以满足条件的最大整数 .
.  (7分)
(7分)

 ,下证当
,下证当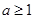 时,在区间
时,在区间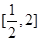 上,函数
上,函数 恒成立.
恒成立.
当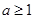 且
且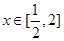 时,
时, ,
,
记 ,
, ,
, 
当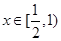 ,
, ;当
;当 ,
,
 ,
,

即对任意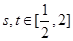 ,都有
,都有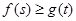 .
.  (12分)
(12分)
方法二:当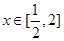 时,
时, 恒成立
恒成立
等价于 恒成立,
恒成立,

当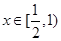 时,
时, ,
, 时,
时,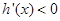 ,
,
即函数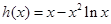 在区间
在区间 上递增,在区间
上递增,在区间 上递减,
上递减,
所以 ,所以
,所以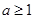 .
.
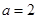 时,
时,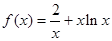 ,
, ,
, ,
, ,
,所以曲线
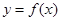 在
在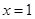 处的切线方程为
处的切线方程为 .
.  (3分)
(3分)
考察
 ,
,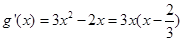 ,
, |  |  | 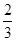 |  |
 |  |  |  |  |
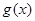 | 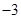 | 递减 | 极(最)小值 | 递增 |
由上表可知:
 ,
, ,
,所以满足条件的最大整数
 .
.  (7分)
(7分)
 ,下证当
,下证当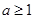 时,在区间
时,在区间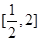 上,函数
上,函数 恒成立.
恒成立.当
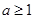 且
且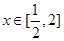 时,
时, ,
,记
 ,
, ,
, 
当
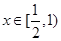 ,
, ;当
;当 ,
, ,
,
即对任意
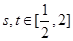 ,都有
,都有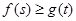 .
.  (12分)
(12分)方法二:当
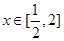 时,
时, 恒成立
恒成立等价于
 恒成立,
恒成立,
当
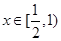 时,
时, ,
, 时,
时,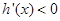 ,
,即函数
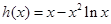 在区间
在区间 上递增,在区间
上递增,在区间 上递减,
上递减,所以
 ,所以
,所以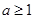 .
. 略

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
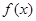 满足
满足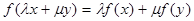 ,
,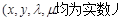 ,则称
,则称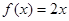 是R上的线性变换
是R上的线性变换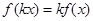
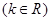
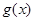 均为R上的线性变换,则
均为R上的线性变换,则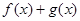 是R上的线性变换
是R上的线性变换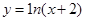 在点P(-1,0)处的切线方程是
在点P(-1,0)处的切线方程是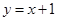
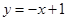
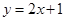
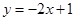
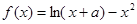 ,
,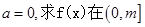
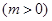 上的最大值
上的最大值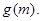
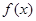 在区间[1,2]上为减函数,求a的取值范围。
在区间[1,2]上为减函数,求a的取值范围。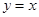 为函数
为函数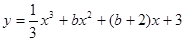 是R上的单调增函数,则
是R上的单调增函数,则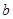 的取值范围是()
的取值范围是()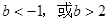
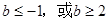
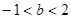
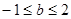
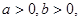 函数
函数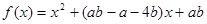 是偶函数,则
是偶函数,则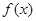 的图象与
的图象与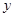 轴交点纵坐标的最小值为
轴交点纵坐标的最小值为
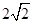
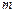 ,A、B相距100
,A、B相距100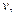 游泳速度为
游泳速度为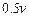 .
.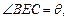 试将此人按上述路线从A到C所需时间T表示为
试将此人按上述路线从A到C所需时间T表示为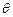 的函数,并求自变量
的函数,并求自变量

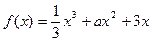 在(0,1)上不是单调函数,则实数a的取值范围为
在(0,1)上不是单调函数,则实数a的取值范围为