题目内容
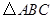 中角
中角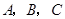 的对边分别为
的对边分别为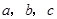 ,
,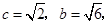 ,
,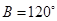 ,则
,则 为( )
为( )
A. | B.2 | C. | D.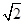 |
D
解析试题分析:在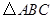 中,由正弦定理可得:
中,由正弦定理可得: ,因为
,因为 ,所以
,所以 ,所以
,所以 所以
所以
考点:本小题主要考查正弦定理在解三角形中的应用,考查学生的运算求解能力.
点评:用正弦定理解三角形,要判断解的个数,利用的工具就是“大边对大角”.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数 的取值分别是( )
的取值分别是( )
A. | B. |
C. | D. |
设 是△
是△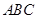 内一点,且
内一点,且 ,
, ,定义
,定义 ,其中
,其中 、
、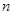 、
、 分别是△
分别是△ 、△
、△ 、△
、△ 的面积,若
的面积,若 , 则
, 则 的最小值是( )
的最小值是( )
| A.8 | B.9 | C. 16 | D.18 |
在平行四边形ABCD中, ,则锐角A的最大值为( )
,则锐角A的最大值为( )
A.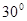 | B.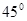 | C. | D.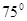 |
若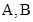 为锐角三角形
为锐角三角形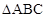 的两个内角,则点
的两个内角,则点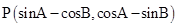
位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
要得到函数 的图象,可将
的图象,可将 的图象
的图象
A.向右平移 个单位 个单位 | B.向左平移 个单位 个单位 |
C.向上平移 个单位 个单位 | D.向下平移 个单位 个单位 |
函数 定义域为
定义域为 ,值域为
,值域为 ,则
,则 的最大值与最小值之和为( )
的最大值与最小值之和为( )
A. | B. | C. | D. |
 的值是( ).
的值是( ).
A. | B. | C.0 | D.1 |
 是实数,则函数
是实数,则函数 的图象不可能是( )
的图象不可能是( )