题目内容
在曲线C1:
(θ为参数,0≤θ<2π)上求一点,使它到直线C2:
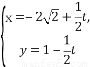(t为参数)的距离最小,并求出该点坐标和最小距离.
(1-
,-) 最小值1
【解析】直线C2化成普通方程是x+y-1+2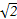
=0,
设所求的点为P(1+cosθ,sinθ),
则P到直线C2的距离
d=
=|sin(θ+
)+2|,
当θ+=
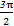时,即θ=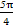
时,d取最小值1,
此时,点P的坐标是(1-,-).
练习册系列答案
相关题目
题目内容
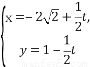在曲线C1:(θ为参数,0≤θ<2π)上求一点,使它到直线C2:(t为参数)的距离最小,并求出该点坐标和最小距离.
(1-,-) 最小值1
【解析】直线C2化成普通方程是x+y-1+2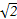=0,
设所求的点为P(1+cosθ,sinθ),
则P到直线C2的距离
d=
=|sin(θ+)+2|,
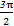当θ+=时,即θ=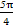时,d取最小值1,
此时,点P的坐标是(1-,-).
