题目内容
如图,三角形ABC中,AC=BC=![]() ,ABED是边长为
,ABED是边长为![]() 的正方形,平面ABED⊥底面ABC,且,若G、F分别是EC、BD的中点,
的正方形,平面ABED⊥底面ABC,且,若G、F分别是EC、BD的中点,
(Ⅰ)求证:GF//底面ABC;
(Ⅱ)求证:平面EBC⊥平面ACD;
(Ⅲ)求几何体ADEBC的体积V。

平面EBC⊥平面ACD
解析:
(I)证法一:取BE的中点H,连结HF、GH,
∵G、F分别是EC和BD的中点
∴HG//BC,HF//DE,
又∵ADEB为正方形 ∴DE//AB,从而HF//AB
∴HF//平面ABC,HG//平面ABC
∴平面HGF//平面ABC
∴GF//平面ABC
证法二:取BC的中点M,AB的中点N连结GM、FN、MN
∵G、F分别是EC和BD的中点
![]() ∴
∴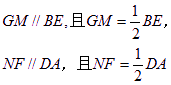
又∵ADEB为正方形 ∴BE//AD,BE=AD
∴GM//NF且GM=NF
∴MNFG为平行四边形
∴GF//MN,又![]() ,
,
∴GF//平面ABC
(Ⅱ)∵ADEB为正方形,∴EB⊥AB
又∵平面ABED⊥平面ABC,∴BE⊥平面ABC …
∴BE⊥AC 又∵CA2+CB2=AB2
∴AC⊥BC ∴AC⊥平面BCE
从而平面EBC⊥平面ACD
(Ⅲ)连结CN,因为AC=BC,所以CN⊥AB,且![]()
又平面ABED⊥平面ABC,
所以CN⊥平面ABED。
∵C—ABED是四棱锥
∴VC—ABED=![]()
![]()

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 如图,三角形ABC中,AB=AC,⊙O经过点A,与BC相切于B,与AC相交于D,若AD=CD=1,则⊙O的半径r=
如图,三角形ABC中,AB=AC,⊙O经过点A,与BC相切于B,与AC相交于D,若AD=CD=1,则⊙O的半径r=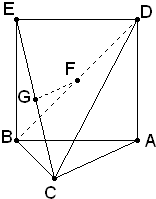 如图,三角形ABC中,AC=BC=
如图,三角形ABC中,AC=BC= 如图,三角形ABC中,
如图,三角形ABC中, 如图在三角形ABC中,E为斜边AB的中点,CD⊥AB,AB=1,则
如图在三角形ABC中,E为斜边AB的中点,CD⊥AB,AB=1,则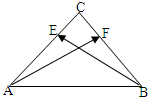 如图直角三角形ABC中,|CA|=|CB|,|AB|=3,点E1,F分别在CA、CB上,EF∥AB,
如图直角三角形ABC中,|CA|=|CB|,|AB|=3,点E1,F分别在CA、CB上,EF∥AB,