题目内容
 如图,三角形ABC中,AB=AC,⊙O经过点A,与BC相切于B,与AC相交于D,若AD=CD=1,则⊙O的半径r=
如图,三角形ABC中,AB=AC,⊙O经过点A,与BC相切于B,与AC相交于D,若AD=CD=1,则⊙O的半径r=分析:首先根据圆的切割线定理,写出比例式,求出CB的长,知道三角形的三条边长再由余弦定理求出角A的余弦值,进而求出正弦值,根据正弦定理求出圆的半径.
解答:解:∵CB是圆的切线,CDA是圆的割线,
∴CB2=CD•CA=1×2=2,
∴CB=
,
在等腰三角形ABC中,
由余弦定理知cosA=
=
,
∴sinA=
=
,
根据正弦定理
=2r,
∴r=
,
故答案为:
∴CB2=CD•CA=1×2=2,
∴CB=
| 2 |
在等腰三角形ABC中,
由余弦定理知cosA=
| 4+4-2 |
| 2×2×2 |
| 3 |
| 4 |
∴sinA=
1-
|
| ||
| 4 |
根据正弦定理
| ||||
|
∴r=
2
| ||
| 7 |
故答案为:
2
| ||
| 7 |
点评:本题是一个非常好的题目,因为要考查与圆有关的比例线段,考查正弦定理和余弦定理,其中这两个定理所占的比重比较大,注意定理的使用.

练习册系列答案
相关题目
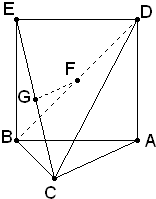 如图,三角形ABC中,AC=BC=
如图,三角形ABC中,AC=BC= 如图,三角形ABC中,
如图,三角形ABC中, 如图在三角形ABC中,E为斜边AB的中点,CD⊥AB,AB=1,则
如图在三角形ABC中,E为斜边AB的中点,CD⊥AB,AB=1,则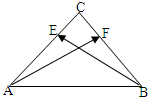 如图直角三角形ABC中,|CA|=|CB|,|AB|=3,点E1,F分别在CA、CB上,EF∥AB,
如图直角三角形ABC中,|CA|=|CB|,|AB|=3,点E1,F分别在CA、CB上,EF∥AB,