题目内容
己知圆 的参数方程为
的参数方程为 (
( 为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆
为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为 .
.
(1)将圆 的参数方程他为普通方程,将圆
的参数方程他为普通方程,将圆 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)圆 ,
, 是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
(1) ,
, ;(2)相交,
;(2)相交,
解析试题分析:(1)利用 消去参数得
消去参数得 由
由 两边同时乘以
两边同时乘以 ,并结合
,并结合 ,
, ,
, 得
得 ;(2)计算圆心距与半径和、差的关系,可判断两圆相交,首先求相交弦所在直线方程,然后放在一个圆中利用垂径定理结合勾股定理求解.
;(2)计算圆心距与半径和、差的关系,可判断两圆相交,首先求相交弦所在直线方程,然后放在一个圆中利用垂径定理结合勾股定理求解.
试题解析:(1)由 得
得 2分
2分
又

 即
即 5分
5分
(2)圆心距 得两圆相交, 6分
得两圆相交, 6分
由 得直线
得直线 的方程为
的方程为 7分
7分
所以,点 到直线
到直线 的距离为
的距离为 8分
8分 10分
10分
考点:1、圆的极坐标方程和参数方程;2、点到直线的距离公式;3、垂径定理.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
两直线 与
与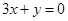 的位置关系是
的位置关系是
| A.相交 | B.平行 | C.重合 | D.平行或重合 |
如果圆 上总存在到原点的距离为
上总存在到原点的距离为 的点,
的点,
则实数 的取值范围是 ( )
的取值范围是 ( )
A. | B. |
| C.[-1, 1] | D. |
下面一段程序执行后输出结果是( )
A=2
A=A*2
A=A+6
PRINT A
| A.2 | B.8 | C.10 | D.18 |
 ,
, ,若
,若 ,则
,则 .
. =2
=2 时,求直线l的方程;
时,求直线l的方程; 是否与直线l的倾斜角有关,若无关,请求出其值;若有关,请说明理由.
是否与直线l的倾斜角有关,若无关,请求出其值;若有关,请说明理由.
 ,如果存在,求出m的值,如果不存在,请说明理由.
,如果存在,求出m的值,如果不存在,请说明理由. 的焦点为
的焦点为 ,经过点
,经过点 的直线
的直线 与抛物线相交于
与抛物线相交于 两点且点
两点且点 恰为
恰为 的中点,则
的中点,则 .
. 的准线与直线
的准线与直线 以及
以及 轴围成三角形面积为
轴围成三角形面积为 ,则
,则