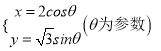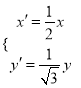题目内容
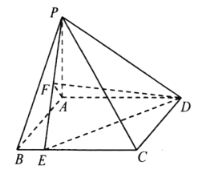
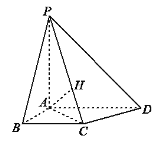
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
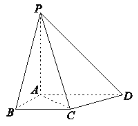
(1)求证:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
【答案】(1)见解析(2)在棱![]() 上存在点
上存在点![]() ,
,![]() ,使得
,使得![]() 平面
平面![]() .
.
【解析】
(1)由题意,利用勾股定理可得![]() ,可得
,可得![]() ,可得
,可得![]() ,利用线面垂直的性质可得
,利用线面垂直的性质可得![]() ,利用线面垂直的判定定理即可证明DC⊥平面PAC;
,利用线面垂直的判定定理即可证明DC⊥平面PAC;
(2)过点A作AH⊥PC,垂足为H,由(1)利用线面垂直的判定定理可证明AH⊥平面PCD,在RT△PAC中,由PA=2,![]() ,可求
,可求![]() ,即在棱PC上存在点H,且
,即在棱PC上存在点H,且![]() ,使得AH⊥平面PCD.
,使得AH⊥平面PCD.
解(1)由题意,可得![]() ,
,
∴![]() ,即
,即![]() ,
,
又![]() 底面
底面![]() ,
,
∴![]() ,
,
且![]() ,
,
∴![]() 平面
平面![]() ;
;
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
由(1)可得![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() .
.
在![]() 中,∵
中,∵![]() ,
,![]() ,
,![]()
∴![]() .
.
即在棱![]() 上存在点
上存在点![]() ,且
,且![]() ,使得
,使得![]() 平面
平面![]() .
.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目