题目内容
已知锐角△ABC中内角A、B、C的对边分别为a、b、c,且sin2A+sin2B=sin2C+sinAsinB.
(1)求角C的值;
(2)设函数 ,且f(x)图象上相邻两最高点间的距离为π,求f(A)的取值范围.
,且f(x)图象上相邻两最高点间的距离为π,求f(A)的取值范围.
解:(1)∵sin2A+sin2B=sin2C+sinAsinB
∴由正弦定理化简已知的等式得:a2+b2=c2+ab,即a2+b2-c2=ab,
∴cosC= =
=
∵0<C< ,∴C=
,∴C= ;
;
(2) =
=
∵f(x)图象上相邻两最高点间的距离为π,
∴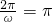 ,∴ω=2,∴f(A)=
,∴ω=2,∴f(A)=
∵C= ,B=
,B=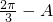 ,0<A<
,0<A< ,0<B<
,0<B<
∴ <A<
<A< ,∴0<2A-
,∴0<2A- <
< ,
,
∴
∴0<f(A)≤ .
.
分析:(1)先根据正弦定理找到角与边的关系,然后再用余弦定理可求出角C的余弦值,从而得到答案;
(2)先确定函数解析式,再确定角的范围,利用三角函数图象的性质,即可得到结论.
点评:本题考查正弦定理的运用,考查三角函数图象的性质,考查学生的计算能力,属于中档题.
∴由正弦定理化简已知的等式得:a2+b2=c2+ab,即a2+b2-c2=ab,
∴cosC=
 =
=
∵0<C<
 ,∴C=
,∴C= ;
;(2)
 =
=
∵f(x)图象上相邻两最高点间的距离为π,
∴
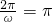 ,∴ω=2,∴f(A)=
,∴ω=2,∴f(A)=
∵C=
 ,B=
,B=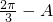 ,0<A<
,0<A< ,0<B<
,0<B<
∴
 <A<
<A< ,∴0<2A-
,∴0<2A- <
< ,
,∴

∴0<f(A)≤
 .
.分析:(1)先根据正弦定理找到角与边的关系,然后再用余弦定理可求出角C的余弦值,从而得到答案;
(2)先确定函数解析式,再确定角的范围,利用三角函数图象的性质,即可得到结论.
点评:本题考查正弦定理的运用,考查三角函数图象的性质,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
己知在锐角ΔABC中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]()
(I )求角![]() 大小;
大小;
(II)当![]() 时,求
时,求![]() 的取值范围.
的取值范围.

20.如图1,在平面内,![]() 是
是![]() 的矩形,
的矩形,![]() 是正三角形,将
是正三角形,将![]() 沿
沿![]() 折起,使
折起,使![]() 如图2,
如图2,![]() 为
为![]() 的中点,设直线
的中点,设直线![]() 过点
过点![]() 且垂直于矩形
且垂直于矩形![]() 所在平面,点
所在平面,点![]() 是直线
是直线![]() 上的一个动点,且与点
上的一个动点,且与点![]() 位于平面
位于平面![]() 的同侧。
的同侧。
(1)求证:![]() 平面
平面![]() ;
;
(2)设二面角![]() 的平面角为
的平面角为![]() ,若
,若![]() ,求线段
,求线段![]() 长的取值范围。
长的取值范围。


21.已知A,B是椭圆![]() 的左,右顶点,
的左,右顶点,![]() ,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线
,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线![]() 于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
(1)求椭圆C的方程;
 (2)求三角形MNT的面积的最大值
(2)求三角形MNT的面积的最大值
22. 已知函数![]()
![]() ,
,
(Ⅰ)若![]() 在
在![]() 上存在最大值与最小值,且其最大值与最小值的和为
上存在最大值与最小值,且其最大值与最小值的和为![]() ,试求
,试求![]() 和
和![]() 的值。
的值。
(Ⅱ)若![]() 为奇函数:
为奇函数:
(1)是否存在实数![]() ,使得
,使得![]() 在
在![]() 为增函数,
为增函数,![]() 为减函数,若存在,求出
为减函数,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)如果当![]() 时,都有
时,都有![]() 恒成立,试求
恒成立,试求![]() 的取值范围.
的取值范围.
 (2009•杭州二模)如图,在直角坐标系xOy中,锐角△ABC内接于圆x2+y2=1.已知BC平行于x轴,AB所在直线方程为y=kx+m(k>0),记角A,B,C所对的边分别是a,b,c.
(2009•杭州二模)如图,在直角坐标系xOy中,锐角△ABC内接于圆x2+y2=1.已知BC平行于x轴,AB所在直线方程为y=kx+m(k>0),记角A,B,C所对的边分别是a,b,c. ),λ∈R;
),λ∈R;