Question

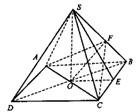正四棱锥S-ABCD中，高SO=2

6

，两相邻侧面所成角为γ，tan

γ

2

=

2 3

3

，
（1）求侧棱与底面所成的角．
（2）求侧棱长、底面边长和斜高（如图）．

Answer 1

分析：（1）在正四棱锥S-ABCD中，侧棱与底面所成的角即为：∠SAO，∠SBO，∠SCO，∠SDO，由已知条件“两相邻侧面所成角为γ，tan

γ

2

=

2 3

3

”可知，得先作出相邻侧面所成二面角的平面角，作CF⊥SB于F，连接AF，易证∠AFC是相邻侧面所成二面角的平面角，在Rt△OFC与Rt△OBF中，可求得∠SBO的大小．
（2）本题的设问是递进式的，第（1）问是为第（2）问作铺垫的．由第（1）问可知：在Rt△SOB、Rt△SEB中，可求得侧棱长、底面边长和斜高．

解答：解：（1）作CF⊥SB于F，连接AF，
则△CFB≌△ABF且AF⊥SB，
故连接OF，则∠AFC=γ，∠OFC=

γ

2

，
在Rt△OFC与Rt△OBF中，tan

γ

2

=

OC

OF

=

OB

OF

=

1

sinα

（其中∠SBO为SB与底面所成的角，设为α）故sinα=

3

2

，α=60°．
（2）在Rt△SOB中，侧棱SB=

SO

sina

=4

2

，OB=SO•cotα=2

2

，
∴边长BC=

2

•OB=4；取BC的中点E，连接SE，则SE是正四棱锥的斜高，
在Rt△SEB中，斜高SE=

SB2-SE2

=2

7

．

点评：本小题考查空间中的线面关系，直线与平面所成的角、二面角、解三角形等基础知识考查空间想象能力和思维能力．