题目内容
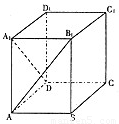
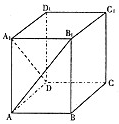 如图,在高为4的长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,则直线AB1与DA1所成角的余弦值是( )
如图,在高为4的长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,则直线AB1与DA1所成角的余弦值是( )A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:连接B1C,AC,由正方体的几何特征,可得∠AB1C即为直线AB1与DA1所成角,根据已知中长方体ABCD-A1B1C1D1的高为4,底面ABCD是边长为2的正方形,求出△AB1C中各边的长,解△AB1C即可得到直线AB1与DA1所成角的余弦值.
解答:解:连接B1C,AC
由正方体的几何特征,可得AB1∥B1C
则∠AB1C即为直线AB1与DA1所成角
∵长方体ABCD-A1B1C1D1的高为4,底面ABCD是边长为2的正方形,
则AB1=B1C=2
,AC=2
∴cos∠AB1C=
=
故选C
由正方体的几何特征,可得AB1∥B1C
则∠AB1C即为直线AB1与DA1所成角
∵长方体ABCD-A1B1C1D1的高为4,底面ABCD是边长为2的正方形,
则AB1=B1C=2
| 5 |
| 2 |
∴cos∠AB1C=
| 20+20-8 |
| 2•20 |
| 4 |
| 5 |
故选C
点评:本题考查的知识点是异面直线及其所成的角,其中结合正方体的几何特征得到∠AB1C即为直线AB1与DA1所成角,是解答本题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
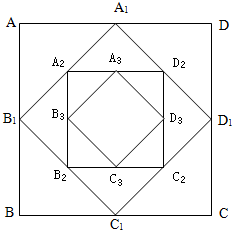 如图,在面积为4的正方形ABCD中,连接各边中点得正方形A1B1C1D1,此时正方形A1B1C1D1的面积记作a1;再连接正方形A1B1C1D1各边中点得正方形A2B2C2D2,此时正方形A2B2C2D2的面积记作a2;…;如此继续下去,得到一个数列{an}.
如图,在面积为4的正方形ABCD中,连接各边中点得正方形A1B1C1D1,此时正方形A1B1C1D1的面积记作a1;再连接正方形A1B1C1D1各边中点得正方形A2B2C2D2,此时正方形A2B2C2D2的面积记作a2;…;如此继续下去,得到一个数列{an}.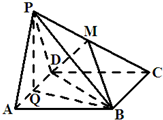 如图,边长为4的正方形ABCD所在平面与正三角形PAD所在平面互相垂直,M,Q分别为PC,AD的中点,
如图,边长为4的正方形ABCD所在平面与正三角形PAD所在平面互相垂直,M,Q分别为PC,AD的中点,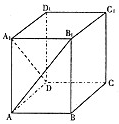 如图,在高为4的长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,则直线AB1与DA1所成角的余弦值是
如图,在高为4的长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,则直线AB1与DA1所成角的余弦值是