题目内容
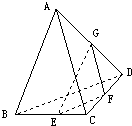E、F、G分别是空间四边形ABCD的棱BC、CD、DA的中点，则此四面体中与过E、F、G的截面平行的棱的条数是（ ）| A、0 | B、1 | C、2 | D、3 |
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：由三角形中位线定理和直线与平面平行的判定定理得AC∥平面EFG，BD∥平面EFG．
解答：
解：在△ACD中，
∵G，F分别为AD与CD的中点，
∴GF∥AC．而GF平面EFG，
∴AC∥平面EFG．
同理，BD∥平面EFG．
故选：C．
∵G，F分别为AD与CD的中点，
∴GF∥AC．而GF平面EFG，
∴AC∥平面EFG．
同理，BD∥平面EFG．
故选：C．
点评：本题考查与平面平行的棱的条数的判断，是中档题，解题时要注意空间思维能力的培养．
练习册系列答案
阅读快车系列答案
相关题目
已知2
+
=（0，1），
=（1，-1），
•
=1，|
|=3，则
与
的夹角为 （ ）
| a |
| b |
| c |
| a |
| c |
| b |
| b |
| c |
A、
| ||
B、
| ||
C、
| ||
D、
|
如果一条直线和一个平面平行，那么这条直线和这个平面内的直线（ ）
| A、相交 | B、平行 |
| C、异面 | D、平行或异面 |
已知
=
，则cot(
+A)的值等于（ ）
| 1-tanA |
| 1+tanA |
| 5 |
| π |
| 4 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
设a=0.22，b=20.2，c=1g（a+b-1），则a、b、c的大小关系为（ ）
| A、a＞b＞c |
| B、b＞c＞a |
| C、c＞b＞a |
| D、b＞a＞c |