题目内容
已知2
+
=(0,1),
=(1,-1),
•
=1,|
|=3,则
与
的夹角为 ( )
| a |
| b |
| c |
| a |
| c |
| b |
| b |
| c |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:数量积表示两个向量的夹角
专题:平面向量及应用
分析:利用向量的数量积的公式以及坐标运算解答.
解答:
解:因为2
+
=(0,1),
=(1,-1),
•
=1,|
|=3,
所以(2
+
)•
=-1=2
•
+
•
=2+
•
,所以
•
=-3,又|
=|=
,|
|=3,
所以
与
的夹角cos<
,
>=
=
=-
,
所以
与
的夹角为
;
故选C.
| a |
| b |
| c |
| a |
| c |
| b |
所以(2
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| b |
| c |
| b |
| c |
| c |
| 2 |
| b |
所以
| b |
| c |
| b |
| c |
| ||||
|
|
| -3 | ||
3
|
| ||
| 2 |
所以
| b |
| c |
| 3π |
| 4 |
故选C.
点评:本题考查了向量的数量积坐标运算以及运用数量积公式求向量的夹角,属于基础题.

练习册系列答案
相关题目
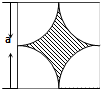 如图所示,墙上挂有边长为a的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为
如图所示,墙上挂有边长为a的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为| a |
| 2 |
A、
| ||
B、1-
| ||
C、1-
| ||
| D、与a的取值有关 |




 在直三棱柱ABC-A1B1C1中,A1A=AB=3
在直三棱柱ABC-A1B1C1中,A1A=AB=3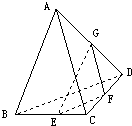 E、F、G分别是空间四边形ABCD的棱BC、CD、DA的中点,则此四面体中与过E、F、G的截面平行的棱的条数是( )
E、F、G分别是空间四边形ABCD的棱BC、CD、DA的中点,则此四面体中与过E、F、G的截面平行的棱的条数是( )