题目内容
抛物线y2=2x上一点M到焦点的距离为1,则点M的横坐标是
.
| 1 |
| 2 |
| 1 |
| 2 |
分析:由抛物线方程,求出焦点F(
,0).设M(x0,y0),由|MF|=1结合两点的距离公式,列式并解之即可得到点M的横坐标.
| 1 |
| 2 |
解答:解:∵抛物线方程为y2=2x,
∴抛物线的焦点F(
,0)
设点M(x0,y0),得|MF|=
=1
将y02=2x0代入,得
=1,
平方得:(x0+
)2=1,解之得x0=
(舍负)
故答案为:
∴抛物线的焦点F(
| 1 |
| 2 |
设点M(x0,y0),得|MF|=
(x0-
|
将y02=2x0代入,得
(x0-
|
平方得:(x0+
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题给出抛物线上一点到焦点的距离,求该点的横坐标.考查了抛物线的定义与标准方程,抛物线的简单几何性质等知识,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
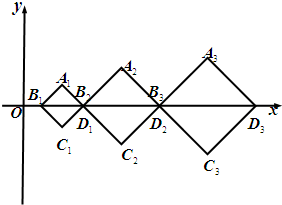 (2009•上海)如图,在直角坐标系xOy中,有一组对角线长为an的正方形AnBnCnDn(n=1,2,…),其对角线BnDn依次放置在x轴上(相邻顶点重合).设{an}是首项为a,公差为d(d>0)的等差数列,点B1的坐标为(d,0).
(2009•上海)如图,在直角坐标系xOy中,有一组对角线长为an的正方形AnBnCnDn(n=1,2,…),其对角线BnDn依次放置在x轴上(相邻顶点重合).设{an}是首项为a,公差为d(d>0)的等差数列,点B1的坐标为(d,0).