题目内容
已知M(a,2)是抛物线y2=2x上的一个定点,直线MP、MQ的倾斜角之和为180°,且与抛物线分别交于P、Q两个不同的点.(1)求a的值;
(2)求证:满足条件的直线PQ是一组平行直线.
分析:(1)将M代入抛物线求出a即可,
(2)利用直线MP,MQ的倾斜角的和为π则其斜率互为相反数,设出MP的方程,将方程与抛物线的方程联立,利用韦达定理求出P的纵坐标与k的关系;同理得到Q的纵坐标与k的关系;利用两点连线的斜率公式求出PQ的斜率即得.
(2)利用直线MP,MQ的倾斜角的和为π则其斜率互为相反数,设出MP的方程,将方程与抛物线的方程联立,利用韦达定理求出P的纵坐标与k的关系;同理得到Q的纵坐标与k的关系;利用两点连线的斜率公式求出PQ的斜率即得.
解答: 解:(1):将点M(a,2)的坐标代入抛物线方程,
解:(1):将点M(a,2)的坐标代入抛物线方程,
得4=2a,∴a=2,即为所求.(4分)
(2)证明:依题意,
直线MP和直线MQ的倾斜角均不为0°和90°,即它们的斜率均在且不为0.(5分)设kMP=
,kMQ=-
,(m≠0)
则直线MP的方程为m(y-2)=x-2,直线MQ的方程为-m(y-2)=x-2,(7分)
由
得:P(2(m+1)2,2(m-1));由
得点Q的坐标为(2(m+1)2,-2(m+1)).(11分)
从而kPQ=
=-
(常数)(13分)
故直线PQ是一组平行直线.(14分)
 解:(1):将点M(a,2)的坐标代入抛物线方程,
解:(1):将点M(a,2)的坐标代入抛物线方程,得4=2a,∴a=2,即为所求.(4分)
(2)证明:依题意,
直线MP和直线MQ的倾斜角均不为0°和90°,即它们的斜率均在且不为0.(5分)设kMP=
| 1 |
| m |
| 1 |
| m |
则直线MP的方程为m(y-2)=x-2,直线MQ的方程为-m(y-2)=x-2,(7分)
由
|
|
得点Q的坐标为(2(m+1)2,-2(m+1)).(11分)
从而kPQ=
| 2(m-1)-[-2(m+1)] |
| 2(m-1)2-2(m+1)2 |
| 1 |
| 2 |
故直线PQ是一组平行直线.(14分)
点评:本题考查解决直线与圆锥曲线的位置关系常用的方法是将它们的方程联立,通过韦达定理得到交点的坐标的关系、考查两点连线的斜率公式.

练习册系列答案
相关题目
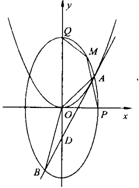 已知点D(0,-2),过点D作抛线C1:x2=2py(p>0)的切线l,切点A在第一象限,如图.
已知点D(0,-2),过点D作抛线C1:x2=2py(p>0)的切线l,切点A在第一象限,如图.
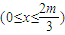 和椭圆弧
和椭圆弧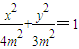

 和椭圆弧
和椭圆弧
