��Ŀ����
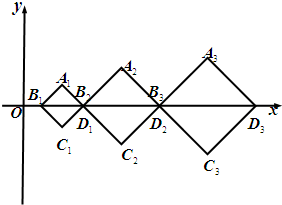 ��2009•�Ϻ�����ͼ����ֱ������ϵxOy�У���һ��Խ��߳�Ϊan��������AnBnCnDn��n=1��2����������Խ���BnDn���η�����x���ϣ����ڶ����غϣ�����{an}������Ϊa������Ϊd��d��0���ĵȲ����У���B1������Ϊ��d��0����
��2009•�Ϻ�����ͼ����ֱ������ϵxOy�У���һ��Խ��߳�Ϊan��������AnBnCnDn��n=1��2����������Խ���BnDn���η�����x���ϣ����ڶ����غϣ�����{an}������Ϊa������Ϊd��d��0���ĵȲ����У���B1������Ϊ��d��0������1����a=8��d=4ʱ��֤��������A1��A2��A3����ͬһ��ֱ���ϣ�
��2���ڣ�1���������£�֤�������ж���An������������y2=2x�ϣ�
��3��Ϊʹ���ж���An������������y2=2px��p��0���ϣ���a��d֮����Ӧ����Ĺ�ϵʽ��
��������1�����A1A2��A1A3��б�ʣ�����б�ʲ���ȣ����ɵõ����ۣ�
��2��ȷ������An�ĺ����ꡢ�����꣬����֤�ý��ۣ�
��3������An�ĺᡢ�����꣬��ȥn-1���������ж���An������������y2=2px��p��0���ϣ�������a��d֮����Ӧ����Ĺ�ϵʽ��
��2��ȷ������An�ĺ����ꡢ�����꣬����֤�ý��ۣ�
��3������An�ĺᡢ�����꣬��ȥn-1���������ж���An������������y2=2px��p��0���ϣ�������a��d֮����Ӧ����Ĺ�ϵʽ��
�����1��֤�����������֪��A1��8��4����A2��18��6����A3��32��8����
��kA1A2=
=
��kA1A3=
=
��
��kA1A2��kA1A3��
�ඥ��A1��A2��A3����ͬһ��ֱ���ϣ�
��2��֤�����������֪������An�ĺ�����xn=d+a1+a2+��+an-1+
an=2��n+1��2��
����An��������yn=
an=2(n+1)��
�߶�����������n����An��xn��yn�����������㷽��y2=2x��
�����ж���An������������y2=2x�ϣ�
��3���⣺�������֪������An�ĺᡢ������ֱ���xn=d+
a+
(n-1)2d��yn=
[a+(n-1)d]
��ȥn-1���ɵ�xn=
yn2+d+
Ϊʹ�����ж���An������������y2=2px��p��0���ϣ�����
��֮����d=4p��a=8p��
��a��d��Ӧ����Ĺ�ϵʽ�ǣ�a=2d��
��kA1A2=
| 6-4 |
| 18-8 |
| 1 |
| 5 |
| 8-6 |
| 32-18 |
| 1 |
| 7 |
��kA1A2��kA1A3��
�ඥ��A1��A2��A3����ͬһ��ֱ���ϣ�
��2��֤�����������֪������An�ĺ�����xn=d+a1+a2+��+an-1+
| 1 |
| 2 |
����An��������yn=
| 1 |
| 2 |
�߶�����������n����An��xn��yn�����������㷽��y2=2x��
�����ж���An������������y2=2x�ϣ�
��3���⣺�������֪������An�ĺᡢ������ֱ���xn=d+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��ȥn-1���ɵ�xn=
| 2 |
| d |
| a(d-a) |
| 2d |
Ϊʹ�����ж���An������������y2=2px��p��0���ϣ�����
|
��֮����d=4p��a=8p��
��a��d��Ӧ����Ĺ�ϵʽ�ǣ�a=2d��
���������⿼�������뷽�̣�����ѧ������������������������ѧ���ļ��������������е��⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ��2009•�Ϻ�ģ�⣩��ͼ��A���ⳤΪa���������һ�����㣬���Ӵ˶����������������е������棬������������ж��㶼��˲��������õĸ���������������湲ͬΧ��һ�������壬����ڴ˶����������½��ۣ�����12�����㣻����24���⣻����12���棻�ܱ����Ϊ3a2�������Ϊ
��2009•�Ϻ�ģ�⣩��ͼ��A���ⳤΪa���������һ�����㣬���Ӵ˶����������������е������棬������������ж��㶼��˲��������õĸ���������������湲ͬΧ��һ�������壬����ڴ˶����������½��ۣ�����12�����㣻����24���⣻����12���棻�ܱ����Ϊ3a2�������Ϊ
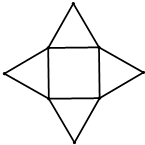 ��2009•�Ϻ�ģ�⣩��ͼ����֪һ���������ƽ��չ��ͼ��һ�߳�Ϊ1���������4���߳�Ϊ1������������ɣ���ö�����������
��2009•�Ϻ�ģ�⣩��ͼ����֪һ���������ƽ��չ��ͼ��һ�߳�Ϊ1���������4���߳�Ϊ1������������ɣ���ö�����������