题目内容
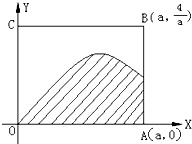如图，矩形OABC内的阴影部分由曲线f（x）=sinx及直线x=a（a∈（0，2π）与x轴围成．向矩形OABC内随机掷一点，该点落在阴影部分的概率为| 1 |
| 2 |
考点：几何概型
专题：概率与统计
分析：根据几何概型的概率公式，以及利用积分求出阴影部分的面积即可得到结论．
解答：
解：根据题意，阴影部分的面积为
sinxdx=-(cosx)
=1-cosa，
矩形的面积为a•
=4，
则由几何概型的概率公式可得
=
，
即cosa=-1，
又a∈（0，2π），
∴a=π，
故答案为：π
| ∫ | a 0 |
| | | a 0 |
矩形的面积为a•
| 4 |
| a |
则由几何概型的概率公式可得
| 1-cosa |
| 4 |
| 1 |
| 2 |
即cosa=-1，
又a∈（0，2π），
∴a=π，
故答案为：π
点评：本题主要考查几何概型的概率的计算，根据积分的几何意义求出阴影部分的面积是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目