题目内容
7．曲线x=|y-1|与y=2x-5围成封闭区域（含边界）为Ω，直线y=3x+b与区域Ω有公共点，则b的最小值为（ ）| A． | 1 | B． | -1 | C． | -7 | D． | -11 |
分析 由约束条件画出平面区域，由y=3x+b得y=3x+B，然后平移直线，利用z的几何意义确定目标函数的最小值即可．
解答 
解：x=|y-1|与y=2x-5围成的平面区域如图，由$\left\{\begin{array}{l}{x=y-1}\\{y=2x-5}\end{array}\right.$，解得A（6，7）
由y=3x+b，
平移直线y=3x+b，则由图象可知当直线经过点A时，
直线y=3x+b的截距最小，此时b最小．
∴b=-3x+y的最小值为-18+7=-11．
故选：D．
点评 本题主要考查线性规划的基本应用，利用目标函数的几何意义是解决问题的关键，数形结合是解决问题的基本方法，是中档题．
练习册系列答案
相关题目
18．设i是虚数单位，则复数（2+i）（1-i）的虚部为（ ）
| A． | i | B． | -1 | C． | 3 | D． | -i |
15．已知等比数列{an}的前n项积为Tn，若log2a2+log2a8=2，则T9的值为（ ）
| A． | ±512 | B． | 512 | C． | ±1024 | D． | 1024 |
2．执行如图所示的程序框图，则输出的S值为（ ）
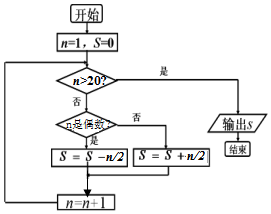
| A． | 10 | B． | -10 | C． | 5 | D． | -5 |
12．已知x∈（$\frac{π}{2}$，π），tanx=-$\frac{4}{3}$，则cos（-x-$\frac{π}{2}$）等于（ ）
| A． | $\frac{3}{5}$ | B． | -$\frac{3}{5}$ | C． | -$\frac{4}{5}$ | D． | $\frac{4}{5}$ |