题目内容
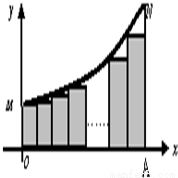
如图，曲线C：y=2x（0≤x≤2）两端分别为M、N，且NA⊥x轴于点A．把线段OA分成n等份，以每一段为边作矩形，使与x轴平行的边一个端点在曲线C上，另一端点在曲线C的下方，设这n个矩形的面积之和为Sn，则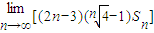
= ．
【答案】分析：根据题意可知从原点出发，矩形的高成等比数列，首项为1，公比为2
，进而根据矩形面积公式，通过等比数列的求和公式求得Sn，最后利用数列极限得出答案．
解答：解：依题意可知从原点出发，矩形的高成等比数列，首项为1，公差为 2
，则
Sn=
[1+2
+
+…+
]=
×
=
×
．
∴
=
=12
故答案为12．．
点评：本题主要考查了等差数列的求和、考查定积分在求面积中的应用等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．
，进而根据矩形面积公式，通过等比数列的求和公式求得Sn，最后利用数列极限得出答案．解答：解：依题意可知从原点出发，矩形的高成等比数列，首项为1，公差为 2
，则Sn=
[1+2++…+]=×=×．∴
==12故答案为12．．
点评：本题主要考查了等差数列的求和、考查定积分在求面积中的应用等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．
练习册系列答案
相关题目
如图，曲线是函数y=Asin（ωx+φ）的图象 （其中A＞0，ω＞0，|φ|＜
（2009•长宁区二模）如图，曲线C：y=2x（0≤x≤2）两端分别为M、N，且NA⊥x轴于点A．把线段OA分成n等份，以每一段为边作矩形，使与x轴平行的边一个端点在曲线C上，另一端点在曲线C的下方，设这n个矩形的面积之和为Sn，则
），则（ ）
，φ=
或ω=
，φ=
,求b的最大值;
a(3a+2)2.
,1),求点D的坐标;
.