题目内容
10.设a,b∈R,则“a>b>1”是“a-b<a2-b2”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 根据不等式的性质,利用充分条件和必要条件的定义进行判断即可得到结论.
解答 解:设命题p:a>b>1;则a-b>0,
命题q:a-b<a2-b2化简得
(a-b)<(a+b)(a-b),
又∵a,b∈R,
∴p⇒q,q推不出p,
∴P是q的充分不必要条件,
即“a>b>1”是“a-b<a2-b2”的充分不必要条件,
故选:A.
点评 本题重点考查充分条件、必要条件和充要条件的概念及其应用,属于中档题

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
5.已知复数z=(3m-2)+(m-1)i,m∈R,i为虚数单位.
(1)当m=2时,求复数z的模|z|;
(2)若z表示纯虚数,求m的值;
(3)在复平面内,若z对应的点位于第三象限,求实数m的取值范围.
(1)当m=2时,求复数z的模|z|;
(2)若z表示纯虚数,求m的值;
(3)在复平面内,若z对应的点位于第三象限,求实数m的取值范围.
7.抛物线x2=$\frac{1}{4}$y的准线方程是( )
| A. | y=1 | B. | y=-1 | C. | y=$\frac{1}{16}$ | D. | y=-$\frac{1}{16}$ |
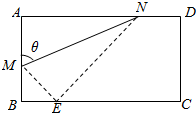 如图,折叠矩形纸片ABCD,使A点落在边BC上的E处,折痕的两端点M、N分别在线段AB和AD上(不与端点重合).已知AB=2,BC=$\frac{{4\sqrt{3}}}{3}$,设∠AMN=θ.
如图,折叠矩形纸片ABCD,使A点落在边BC上的E处,折痕的两端点M、N分别在线段AB和AD上(不与端点重合).已知AB=2,BC=$\frac{{4\sqrt{3}}}{3}$,设∠AMN=θ.