题目内容
20.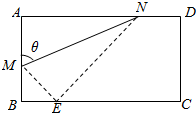 如图,折叠矩形纸片ABCD,使A点落在边BC上的E处,折痕的两端点M、N分别在线段AB和AD上(不与端点重合).已知AB=2,BC=$\frac{{4\sqrt{3}}}{3}$,设∠AMN=θ.
如图,折叠矩形纸片ABCD,使A点落在边BC上的E处,折痕的两端点M、N分别在线段AB和AD上(不与端点重合).已知AB=2,BC=$\frac{{4\sqrt{3}}}{3}$,设∠AMN=θ.(1)用θ表示线段AM的长度,并求出θ的取值范围;
(2)试问折痕MN的长度是否存在最小值,若存在,求出此时cosθ的值;若不存在,请说明理由.
分析 (1)先设出AM,结合图象的对称性得到方程cos(π-2θ)=$\frac{2-x}{x}$,解出即可,再根据AM、AB、AN、AD的关系得到不等式组,解出即可;
(2)先求出MN,通过换元得到$MN=\frac{1}{{t-{t^3}}},t∈(\frac{1}{2},\frac{{\sqrt{2}}}{2})$,设$h(t)=t-{t^3},t∈(\frac{1}{2},\frac{{\sqrt{2}}}{2})$,通过求导得到函数的单调性,从而求出MN的最小值.
解答 解:(1)设AM=x,由图形的对称性可知:AM=ME=x,∠BME=π-2θ,
∵BM=2-x,∴cos(π-2θ)=$\frac{2-x}{x}$,整理得:x=$\frac{2}{1-cos2θ}$=$\frac{1}{{sin}^{2}θ}$,
∵$θ∈(0,\frac{π}{2})$又∵$\left\{{\begin{array}{l}{AM<AB}\\{AN<AD}\end{array}}\right.$,即$\left\{{\begin{array}{l}{\frac{1}{{{{sin}^2}θ}}<2}\\{\frac{1}{{{{sin}^2}θ}}•tanθ<\frac{{4\sqrt{3}}}{3}}\end{array}}\right.$,
∴$\left\{{\begin{array}{l}{sinθ>\frac{{\sqrt{2}}}{2}}\\{sin2θ>\frac{{\sqrt{3}}}{2}}\end{array}}\right.$,$\left\{{\begin{array}{l}{\frac{π}{4}<θ<\frac{π}{2}}\\{\frac{π}{3}<2θ<\frac{2π}{3}}\end{array}}\right.$,解得:$θ∈(\frac{π}{4},\frac{π}{3})$;
(2)在Rt△AMN中,$MN=\frac{x}{cosθ}=\frac{1}{{{{sin}^2}θcosθ}}=\frac{1}{{cosθ-{{cos}^3}θ}}$,$θ∈(\frac{π}{4},\frac{π}{3})$,
令$t=cosθ,t∈(\frac{1}{2},\frac{{\sqrt{2}}}{2})$,
∴$MN=\frac{1}{{t-{t^3}}},t∈(\frac{1}{2},\frac{{\sqrt{2}}}{2})$,
设$h(t)=t-{t^3},t∈(\frac{1}{2},\frac{{\sqrt{2}}}{2})$,
∴h′(t)=1-3t2=-3(t+$\frac{\sqrt{3}}{3}$)(t-$\frac{\sqrt{3}}{3}$),
令h′(t)=0,则t=$\frac{\sqrt{3}}{3}$或t=-$\frac{\sqrt{3}}{3}$(舍),
列表得:
| t | $(\frac{1}{2},\frac{{\sqrt{3}}}{3})$ | $\frac{\sqrt{3}}{3}$ | ($\frac{\sqrt{3}}{3}$,$\frac{\sqrt{2}}{2}$) |
| h′(t) | + | 0 | - |
| h(t) | 增 | 极大值 | 减 |
∴当cosθ=$\frac{\sqrt{3}}{3}$时,MN有最小值为$\frac{3\sqrt{3}}{2}$.
点评 本题考查了三角函数问题,考查导数的应用,考查转化思想,换元思想,是一道中档题.

| A. | 9 | B. | 5 | C. | -5 | D. | -9 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
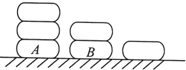 如图,桌面上摆有三串冰糖葫芦,第一串3课,第二串2颗,第三串1颗.小明每次从中取走一颗,若上面的冰糖葫芦取走后才能取下面的冰糖葫芦.则冰糖葫芦A恰好在第五次被取走,且冰糖葫芦B恰好在第六次被取走的取法数为12.
如图,桌面上摆有三串冰糖葫芦,第一串3课,第二串2颗,第三串1颗.小明每次从中取走一颗,若上面的冰糖葫芦取走后才能取下面的冰糖葫芦.则冰糖葫芦A恰好在第五次被取走,且冰糖葫芦B恰好在第六次被取走的取法数为12.