题目内容
(本小题满分14分)
已知函数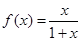
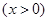 ,数列
,数列 满足:
满足: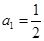 ,
,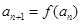
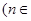 N*
N*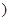 .
.
(1)求数列 的通项公式;
的通项公式;
(2)令函数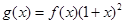 ,数列
,数列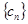 满足:
满足: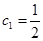 ,
,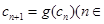 N*),
N*),
求证:对于一切 的正整数,都满足:
的正整数,都满足: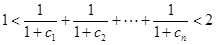 .
.
已知函数
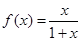
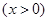 ,数列
,数列 满足:
满足: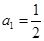 ,
,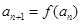
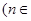 N*
N* .
.(1)求数列
 的通项公式;
的通项公式;(2)令函数
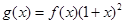 ,数列
,数列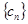 满足:
满足: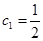 ,
,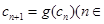 N*),
N*),求证:对于一切
 的正整数,都满足:
的正整数,都满足: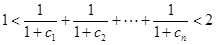 .
.(1) ;(2)见解析。
;(2)见解析。
 ;(2)见解析。
;(2)见解析。本题考查数列的通项公式的求法和数列的前n项和公式的求法,解题时要认真审题,仔细解答,注意合理裂项求和法的合理运用.
(1)因为 ,则
,则 ,得
,得 ,即
,即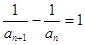 ,∴数列
,∴数列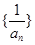 是首项为2、公差为1的等差数列,得到通项公式。
是首项为2、公差为1的等差数列,得到通项公式。
(2)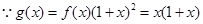 ,故
,故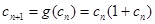 ,又
,又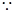
 ,故
,故 ,
,
则 ,即
,即 ,利用裂项法得到和式。
,利用裂项法得到和式。
(1)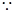
 ,则
,则 ,得
,得 ,即
,即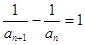 ,∴数列
,∴数列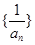 是首项为2、公差为1的等差数列,…………4分
是首项为2、公差为1的等差数列,…………4分
∴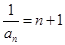 ,即
,即 …………6分
…………6分
(2)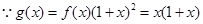 ,故
,故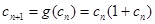 ,又
,又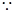
 ,故
,故 ,
,
则 ,即
,即 .…………8分
.…………8分
∴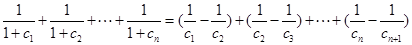
=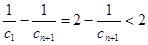 . …………11分
. …………11分
又
 ,………14分
,………14分
故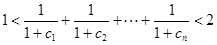 .…………14分
.…………14分
(1)因为
 ,则
,则 ,得
,得 ,即
,即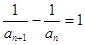 ,∴数列
,∴数列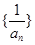 是首项为2、公差为1的等差数列,得到通项公式。
是首项为2、公差为1的等差数列,得到通项公式。(2)
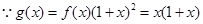 ,故
,故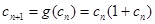 ,又
,又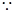
 ,故
,故 ,
,则
 ,即
,即 ,利用裂项法得到和式。
,利用裂项法得到和式。(1)
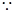
 ,则
,则 ,得
,得 ,即
,即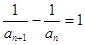 ,∴数列
,∴数列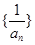 是首项为2、公差为1的等差数列,…………4分
是首项为2、公差为1的等差数列,…………4分∴
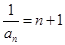 ,即
,即 …………6分
…………6分(2)
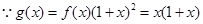 ,故
,故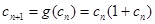 ,又
,又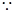
 ,故
,故 ,
,则
 ,即
,即 .…………8分
.…………8分∴
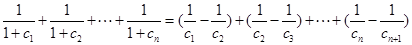
=
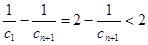 . …………11分
. …………11分又

 ,………14分
,………14分故
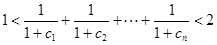 .…………14分
.…………14分
练习册系列答案
相关题目
 的图像经过点
的图像经过点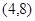 .
.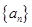 中,若
中,若 ,
,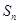 为数列
为数列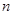 项和,且满足
项和,且满足 ,
,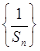 成等差数列,并求数列
成等差数列,并求数列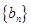 ,若将数列
,若将数列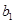
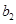
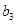
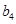
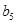
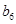
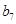
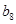

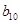
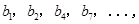 构成的数列即为数列
构成的数列即为数列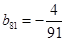 时,求上表中第
时,求上表中第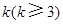 行所有项的和.
行所有项的和.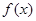 定义在区间
定义在区间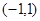 上,
上,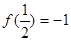 ,且当
,且当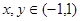 时,
时,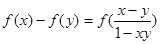 .又数列
.又数列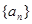 满足
满足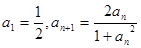 .
.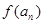 的表达式;
的表达式;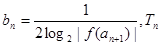 为数列
为数列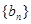 的前
的前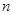 项和,若
项和,若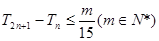 对
对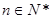 恒成立,求
恒成立,求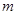 的最小值.
的最小值.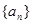 是等差数列,其前n项和为Sn,
是等差数列,其前n项和为Sn,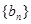 是等比数列,且
是等比数列,且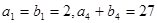 ,
,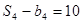 .
.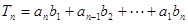 ,
,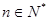 ,求
,求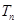 (
(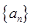 的前n项和
的前n项和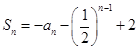 (n为正整数)。
(n为正整数)。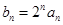 ,求证数列
,求证数列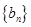 是等差数列,并求数列
是等差数列,并求数列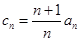 ,
,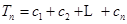 ,求
,求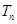 .
.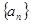 中,
中,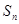 是其前
是其前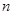 项和,
项和,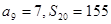 ,求:
,求: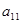 及
及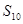 .
.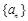 的前n项和为
的前n项和为 ,且
,且 ,
, .
.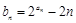 ,求数列
,求数列 的前n项和
的前n项和 .
.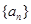 中,若
中,若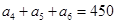 ,则
,则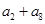 的值为 .
的值为 .