题目内容
已知数列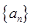 的前n项和
的前n项和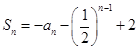 (n为正整数)。
(n为正整数)。
(Ⅰ)令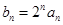 ,求证数列
,求证数列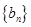 是等差数列,并求数列
是等差数列,并求数列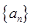 的通项公式;
的通项公式;
(Ⅱ)令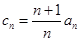 ,
,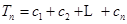 ,求
,求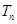 .
.
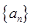 的前n项和
的前n项和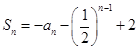 (n为正整数)。
(n为正整数)。(Ⅰ)令
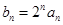 ,求证数列
,求证数列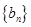 是等差数列,并求数列
是等差数列,并求数列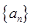 的通项公式;
的通项公式;(Ⅱ)令
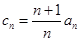 ,
,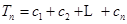 ,求
,求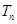 .
.(1) (2)
(2)
 (2)
(2)
试题分析:(I)在
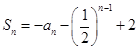 中,令n=1,可得
中,令n=1,可得 ,
,即
 , ---2分
, ---2分当
 时,
时, ,
,
 .
.又因为
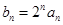 ,所以
,所以 ,即当
,即当 时,
时, .
.又
 数列
数列 是首项和公差均为1的等差数列. ---4分
是首项和公差均为1的等差数列. ---4分于是
 . ---6分
. ---6分(II)由(I)得
 ,所以
,所以
---8分
由①-②得

 ---12分
---12分点评:由已知式子再写一个作差时,要注意n的取值范围;利用错位相减法求数列的前n项和时,方法不难,但是化简容易出错,必须认真计算,此处知识在高考中经常考查.

练习册系列答案
相关题目
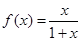
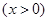 ,数列
,数列 满足:
满足: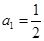 ,
,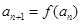
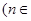 N*
N*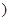 .
.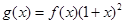 ,数列
,数列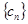 满足:
满足: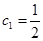 ,
,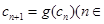 N*),
N*), 的正整数,都满足:
的正整数,都满足: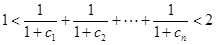 .
. }中,
}中, 则
则
 的等差数列
的等差数列 中,最接近零的是第( ) 项.
中,最接近零的是第( ) 项.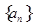 是等差数列,且a2+ a5+ a8+ a11=48,则a6+ a7= ( )
是等差数列,且a2+ a5+ a8+ a11=48,则a6+ a7= ( )  }中,
}中, ,则前10项和
,则前10项和 ( )
( )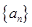 满足
满足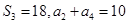 。
。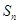 的最大值;
的最大值;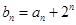 ,求数列
,求数列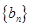 的其前
的其前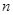 项和
项和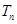 .
. 为等比数列,
为等比数列, 是它的前
是它的前 项和,若
项和,若 ,且
,且 与
与 的等差中项为
的等差中项为 ,则
,则 =
=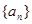 中,已知
中,已知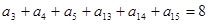 ,则
,则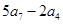 = .
= .