题目内容
试证明:不论正数a、b、c是等差数列还是等比数列,当n>1,n∈N*且a、b、c互不相等时,均有:an+cn>2bn.
见解析
错解分析:应分别证明不等式对等比数列或等差数列均成立,不应只证明一种情况.
技巧与方法:本题中使用到结论:(ak-ck)(a-c)>0恒成立(a、b、c为正数),从而ak+1+ck+1>ak·c+ck·a.
证明:(1)设a、b、c为等比数列,a=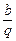 ,c=bq(q>0且q≠1)
,c=bq(q>0且q≠1)
∴an+cn= +bnqn=bn(
+bnqn=bn(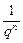 +qn)>2bn
+qn)>2bn
(2)设a、b、c为等差数列,则2b=a+c猜想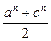 >(
>( )n(n≥2且n∈N*)
)n(n≥2且n∈N*)
下面用数学归纳法证明:
①当n=2时,由2(a2+c2)>(a+c)2,∴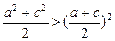
②设n=k时成立,即
则当n=k+1时,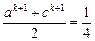 (ak+1+ck+1+ak+1+ck+1)
(ak+1+ck+1+ak+1+ck+1)
>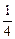 (ak+1+ck+1+ak·c+ck·a)=
(ak+1+ck+1+ak·c+ck·a)=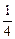 (ak+ck)(a+c)
(ak+ck)(a+c)
>( )k·(
)k·( )=(
)=( )k+1
)k+1
技巧与方法:本题中使用到结论:(ak-ck)(a-c)>0恒成立(a、b、c为正数),从而ak+1+ck+1>ak·c+ck·a.
证明:(1)设a、b、c为等比数列,a=
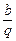 ,c=bq(q>0且q≠1)
,c=bq(q>0且q≠1)∴an+cn=
 +bnqn=bn(
+bnqn=bn(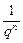 +qn)>2bn
+qn)>2bn(2)设a、b、c为等差数列,则2b=a+c猜想
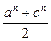 >(
>( )n(n≥2且n∈N*)
)n(n≥2且n∈N*)下面用数学归纳法证明:
①当n=2时,由2(a2+c2)>(a+c)2,∴
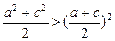
②设n=k时成立,即

则当n=k+1时,
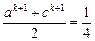 (ak+1+ck+1+ak+1+ck+1)
(ak+1+ck+1+ak+1+ck+1)>
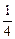 (ak+1+ck+1+ak·c+ck·a)=
(ak+1+ck+1+ak·c+ck·a)=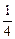 (ak+ck)(a+c)
(ak+ck)(a+c)>(
 )k·(
)k·( )=(
)=( )k+1
)k+1
练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 .
. 的表达式表示
的表达式表示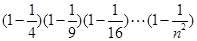 的值,并用数学归纳法证明你的结论.
的值,并用数学归纳法证明你的结论. 时,若已假设n=k(k≥2为偶数)时命题为真,则还需要用归纳假设再证( )
时,若已假设n=k(k≥2为偶数)时命题为真,则还需要用归纳假设再证( )
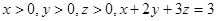 ,那么
,那么 的最小值为 ;
的最小值为 ; ”时,
”时,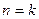 ”变到“
”变到“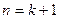 ”时,左边应增乘的因式是_________________;
”时,左边应增乘的因式是_________________;