题目内容
设数列{an}的前n项和为Sn,a1=1,Sn=nan-2n(n-1).
(1)求数列{an}的通项公式an;(2)设数列{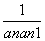 }的前n项和为Tn,求证:
}的前n项和为Tn,求证: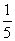 ≤Tn<
≤Tn<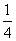 .
.
(1)解 由Sn=nan-2n(n-1)得an+1=Sn+1-Sn=(n+1)an+1-nan-4n,即an+1-an=4.
∴数列{an}是以1为首项,4为公差的等差数列,∴an=4n-3.
(2)证明 Tn= +
+ +…+
+…+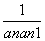 =
= +
+ +
+ +…+
+…+
=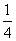 (1-
(1-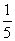 +
+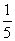 -
- +
+ -
- +…+
+…+ -
- )=
)=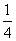 (1-
(1- )<
)<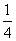 .
.
又易知Tn单调递增,故Tn≥T1=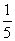 ,得
,得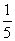 ≤Tn<
≤Tn<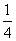 .
.

练习册系列答案
相关题目
 共焦点且过点(5,-2)的双曲线标
共焦点且过点(5,-2)的双曲线标 准方程是( )
准方程是( )

 的前
的前 项和为
项和为 ,若
,若 ,则
,则 ( )
( )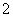 (B)
(B)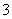 (C)
(C)
 (D)
(D)
 中,已知
中,已知 是边长为1的正方形,且
是边长为1的正方形,且 是正三角形,,
是正三角形,, ,则该多面体的体积为
,则该多面体的体积为 ( )
( ) (B)
(B)  (C)
(C)  (D)
(D)
 .
. 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 时,若
时,若 在区间
在区间 上的最小值为
上的最小值为 ,求
,求 的取值范围.
的取值范围.
 确定的平面区域记为Ω1,不
确定的平面区域记为Ω1,不 等式组
等式组 确定的平面区域记为Ω2,在Ω1中随机取一点,则该点恰好在Ω2内的概率为( )
确定的平面区域记为Ω2,在Ω1中随机取一点,则该点恰好在Ω2内的概率为( )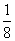 B.
B. C.
C. D.
D.
