题目内容
【题目】己知椭圆W:![]() +
+![]() =1(a>b>0),直线
=1(a>b>0),直线![]() :
:![]() =
=![]() 与
与![]() 轴,
轴,![]() 轴的交点分别是椭圆W的焦点与顶点。
轴的交点分别是椭圆W的焦点与顶点。

(1)求椭圆W的方程;
(2)设直线m:![]() =kx(k≠0)与椭圆W交于P,Q两点,过点P(
=kx(k≠0)与椭圆W交于P,Q两点,过点P(![]() ,
,![]() )作PC⊥轴,垂足为点C,直线
)作PC⊥轴,垂足为点C,直线![]() 交椭圆w于另一点R。
交椭圆w于另一点R。
①求△PCQ面积的最大值;②求出∠QPR的大小。
【答案】(1)![]() ;(2)①
;(2)①![]() ,②90
,②90![]() .
.
【解析】
(1)由题意求出c,b,进而得到椭圆W的方程;
(2)①设P(![]() ,
,![]() ),则Q(
),则Q(![]() ,
,![]() ),C(
),C(![]() ,0),可知S
,0),可知S![]() ,利用点在椭圆上及均值不等式即可得到△PCQ面积的最大值;②设P(
,利用点在椭圆上及均值不等式即可得到△PCQ面积的最大值;②设P(![]() ,
,![]() ),则Q(
),则Q(![]() ,
,![]() ),C(
),C(![]() ,0),k=
,0),k=![]() ,直线QR的斜率
,直线QR的斜率![]() ,直线QR的方程:
,直线QR的方程:![]() (
(![]() )与椭圆方程联立可得(2+
)与椭圆方程联立可得(2+![]() )2-2
)2-2![]() ,求得R点坐标,进而得到
,求得R点坐标,进而得到![]() 即可得到结果.
即可得到结果.
(1)直线![]() :
:![]() 与
与![]() 轴,
轴,![]() 轴的交点分别(
轴的交点分别(![]() ,0),(0,
,0),(0,![]() ),
),
可知c=![]() ,
,![]() ,椭圆W的方程
,椭圆W的方程![]() 。
。
(2)①设P(![]() ,
,![]() ),则Q(
),则Q(![]() ,
,![]() ),C(
),C(![]() ,0),可知S
,0),可知S![]() ,
,
有已知可知![]() ,根据重要不等式得
,根据重要不等式得![]() ,S
,S![]() ,
,
当且仅当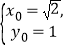 或
或 时,面积取得最大值
时,面积取得最大值![]() 。
。
②设P(![]() ,
,![]() ),则Q(
),则Q(![]() ,
,![]() ),C(
),C(![]() ,0),k=
,0),k=![]() 。
。
直线QR的斜率![]() 。
。
可得直线QR的方程:![]() (
(![]() ),设点R(
),设点R(![]() ,
,![]() ),
),
联立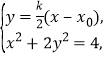 消去
消去![]() 得(2+
得(2+![]() )2-2
)2-2![]() ,
,
则![]() ,解得
,解得![]() ,所以
,所以![]() ,点R(
,点R(![]() ,
,![]() )。
)。
因为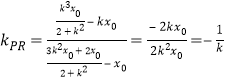 ,所以
,所以![]() ,所以∠QPR=90°。
,所以∠QPR=90°。

练习册系列答案
相关题目
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 5 | ﹣5 | 0 |
(1)请将上表数据补充完整,并直接写出函数f(x)的解析式;
(2)将y=f(x)图象上所有点向左平移θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为(![]() ,0),求θ的最小值.
,0),求θ的最小值.
(3)若![]() ,求
,求![]() 的值.
的值.



