题目内容
观察下列式子: ,…,根据上述规律,第n个不等式应该为________.
,…,根据上述规律,第n个不等式应该为________.
1+ +
+ +…+
+…+ <
<
分析:根据规律,不等式的左边是n+1个自然数倒数的平方的和,右边分母是以2为首项,1为公差的等差数列,分子是以3为首项,2为公差的等差数列,由此可得结论.
解答:根据规律,不等式的左边是n+1个自然数倒数的平方的和,右边分母是以2为首项,1为公差的等差数列,分子是以3为首项,2为公差的等差数列,所以第n个不等式应该为1+ +
+ +…+
+…+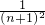 <
<
故答案为:1+ +
+ +…+
+…+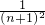 <
<
点评:本题考查归纳推理,考查学生分析解决问题的能力,属于基础题.
 +
+ +…+
+…+ <
<
分析:根据规律,不等式的左边是n+1个自然数倒数的平方的和,右边分母是以2为首项,1为公差的等差数列,分子是以3为首项,2为公差的等差数列,由此可得结论.
解答:根据规律,不等式的左边是n+1个自然数倒数的平方的和,右边分母是以2为首项,1为公差的等差数列,分子是以3为首项,2为公差的等差数列,所以第n个不等式应该为1+
 +
+ +…+
+…+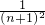 <
<
故答案为:1+
 +
+ +…+
+…+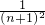 <
<
点评:本题考查归纳推理,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目