题目内容
已知f(x)=loga(1)求函数的定义域;
(2)讨论函数的单调性;
(3)求使f(x)>0的x的取值范围.
解:(1)由 ∴函数的定义域为(-1,1). (2)对任意-1<x1<x2<1, 当a>1时,loga 当0<a<1时,loga ∴当a>1时,f(x)为(-1,1)上的增函数; 当0<a<1时,f(x)为(-1,1)上的减函数. (3)loga ∴当a>1时, ∴2x(x-1)<0.∴0<x<1. 当0<a<1时, 当a>1时,f(x)>0的解为(0,1); 当0<a<1时,f(x)>0的解为(-1,0).
![]() >0得-1<x<1.
>0得-1<x<1.![]() -
-![]() =
=![]() <0,∴
<0,∴![]() <
<![]() .
.![]() <loga
<loga![]() ,即f(x1)<f(x2);
,即f(x1)<f(x2);![]() >loga
>loga![]() ,即f(x1)>f(x2).
,即f(x1)>f(x2).![]() >0= loga 1.
>0= loga 1.![]() >1,即
>1,即![]() -1=
-1=![]() >0.
>0.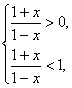 解得-1<x<0;
解得-1<x<0; 练习册系列答案
练习册系列答案
全优AB卷系列答案
品优课堂系列答案
核心课堂武汉大学出版社系列答案
冠军练加考系列答案
考点集训与满分备考系列答案
课堂小测6分钟系列答案

期末满分冲刺阶段练习与单元测试系列答案
轻松15分导学案系列答案
点燃思维全能课时训练系列答案
相关题目
已知f(x)是定义在R上的奇函数,当x>0时,f(x)=log
x,那么f(-
)的值是( )
| 1 |
| 4 |
| 1 |
| 2 |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |