题目内容
已知椭圆C1: ,抛物线C2:(y-m)2=2px(p>0),且C1、C2的公共弦AB过椭圆C1的右焦点。
,抛物线C2:(y-m)2=2px(p>0),且C1、C2的公共弦AB过椭圆C1的右焦点。
(1)当AB⊥x轴时,求m、p的值,并判断抛物线C2的焦点是否在直线AB上;
(2)若 且抛物线C2的焦点在直线AB上,求m的值及直线AB的方程。
且抛物线C2的焦点在直线AB上,求m的值及直线AB的方程。
 ,抛物线C2:(y-m)2=2px(p>0),且C1、C2的公共弦AB过椭圆C1的右焦点。
,抛物线C2:(y-m)2=2px(p>0),且C1、C2的公共弦AB过椭圆C1的右焦点。(1)当AB⊥x轴时,求m、p的值,并判断抛物线C2的焦点是否在直线AB上;
(2)若
 且抛物线C2的焦点在直线AB上,求m的值及直线AB的方程。
且抛物线C2的焦点在直线AB上,求m的值及直线AB的方程。解;(1)当AB⊥x轴时,点A、B关于x轴对称,所以m=0,
直线AB的方程为x=1,从而点A的坐标为(1, )或(1,-
)或(1,- )
)
因为点A在抛物线上,
所以 ,即
,即
此时C2的焦点坐标为( ,0),该焦点不在直线AB上。
,0),该焦点不在直线AB上。
(2)当C2的焦点在AB时,由(1)知直线AB的斜率存在,
设直线AB的方程为
由 消去y得
消去y得 ①
①
设A、B的坐标分别为(x1,y1),(x2,y2),
则x1,x2是方程①的两根,x1+x2=
因为AB既是过C1的右焦点的弦,又是过C2的焦点的弦,
所以 ,且
,且
从而
所以 ,即
,即
解得 ,即
,即
因为C2的焦点 在直线
在直线 上,
上,
所以
即 或
或
当 时,直线AB的方程为
时,直线AB的方程为
当 时,直线AB的方程为
时,直线AB的方程为 。
。
直线AB的方程为x=1,从而点A的坐标为(1,
 )或(1,-
)或(1,- )
)因为点A在抛物线上,
所以
 ,即
,即
此时C2的焦点坐标为(
 ,0),该焦点不在直线AB上。
,0),该焦点不在直线AB上。(2)当C2的焦点在AB时,由(1)知直线AB的斜率存在,
设直线AB的方程为

由
 消去y得
消去y得 ①
①设A、B的坐标分别为(x1,y1),(x2,y2),
则x1,x2是方程①的两根,x1+x2=

因为AB既是过C1的右焦点的弦,又是过C2的焦点的弦,
所以
 ,且
,且
从而

所以
 ,即
,即
解得
 ,即
,即
因为C2的焦点
 在直线
在直线 上,
上,所以

即
 或
或
当
 时,直线AB的方程为
时,直线AB的方程为
当
 时,直线AB的方程为
时,直线AB的方程为 。
。
练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
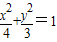 ,抛物线C2:(y-m)2=2px(p>0),且C1、C2的公共弦AB过椭圆C1的右焦点.
,抛物线C2:(y-m)2=2px(p>0),且C1、C2的公共弦AB过椭圆C1的右焦点.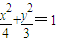 ,抛物线C2:(y-m)2=2px(p>0),且C1、C2的公共弦AB过椭圆C1的右焦点.
,抛物线C2:(y-m)2=2px(p>0),且C1、C2的公共弦AB过椭圆C1的右焦点.