题目内容
已知椭圆C1:(1)当AB⊥x轴时,求m、p的值,并判断抛物线C2的焦点是否在直线AB上;
(2)是否存在m、p的值,使抛物线C2的焦点恰在直线AB上?若存在.求出符合条件的m、p的值;若不存在,请说明理由.
解:(1)当AB⊥x轴时,点A、B关于x轴对称,所以m=0,直线AB的方程x=1,从而点A的坐标为(1,![]() )或(1,
)或(1,![]() ).?
).?
因为点A在抛物线上,所以![]() =2p,即p=
=2p,即p=![]() .此时C2的焦点坐标为(
.此时C2的焦点坐标为(![]() ,0).该焦点不在直线AB上.?
,0).该焦点不在直线AB上.?
(2)解法一:假设存在m、p的值使C2的焦点恰在直线AB上,由(1)知直线AB的斜率存在,故可设直线AB的方程为y=k(x-1).?
由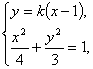
消去y得(3+4k2)x2-8k2x+4k2-12=0. ①?
设A、B的坐标分别为(x1,y1)、(x2、y2),则x1、x2是方程①的两根,x1+x2=![]() ,
,
由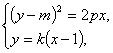 消去y得(kx-k-m)2=2px. ②?
消去y得(kx-k-m)2=2px. ②?
因为C2的焦点F′(![]() ,m)在y=k(x-1)上,?
,m)在y=k(x-1)上,?
所以m=k(![]() -1),即m+k=
-1),即m+k=![]() ,?
,?
代入②有(kx-![]() ) 2=2px,?
) 2=2px,?
即k2x2-p(k2+2)x+![]() . ③?
. ③?
由于x1、x2也是方程③的两根,?
所以x1+x2=![]() ,?
,?
从而![]() ,p=
,p=![]() . ④?
. ④?
又AB过C1、C2的焦点,?
所以|AB|=(x1+![]() )+(x2+
)+(x2+![]() )=x1+x2+p=(2-
)=x1+x2+p=(2-![]() x1)+(2-
x1)+(2-![]() x2).?
x2).?
则p=4-![]() (x1+x2)=
(x1+x2)=![]() . ⑤?
. ⑤?
由④⑤得![]() ,
,
即k4-5k2-6=0,解得k2=6,于是k=±![]() ,p=
,p=![]() .?
.?
因为C2的焦点F(![]() ,m)在直线y=±
,m)在直线y=±![]() (x-1)上,?
(x-1)上,?
所以m=±![]() (
(![]() -1),即m=
-1),即m=![]() 或m=-
或m=-![]() ,由上知,满足条件的m、p存在,且m=
,由上知,满足条件的m、p存在,且m=![]() 或m=-
或m=-![]() ,p=
,p=![]() .?
.?
解法二:设A、B的坐标分别为(x1,y1)、(x2,y2),?
因为AB既过C1的右焦点F(1,0),又过C2的焦点F′(![]() ,m)?
,m)?
所以|AB|=(x1+![]() )+(x2+
)+(x2+![]() )=x1+x2+p=(2-
)=x1+x2+p=(2-![]() x1)+(2-
x1)+(2-![]() x2).?
x2).?
即x1+x2=![]() (4-p). ①?
(4-p). ①?
由(1)知x1≠x2,p≠2,于是直线AB的斜率?
k=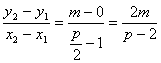 , ②?
, ②?
且直线AB的方程是y=![]() (x-1),?
(x-1),?
所以y1+y2=![]() (x1+x2-2)=
(x1+x2-2)=![]() . ③?
. ③?
又因为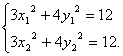
所以3(x1+x2)+4(y1+y2)·![]() =0. ④?
=0. ④?
将①②③代入④得m2=![]() . ⑤?
. ⑤?
因为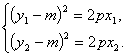 ?
?
所以y1+y2-2m=2p![]() , ⑥?
, ⑥?
将②③代入⑥得m2=![]() . ⑦?
. ⑦?
由⑤⑦得![]() .?
.?
即3p2+20p-32=0.?
解得p=![]() 或p=-8(舍去)?
或p=-8(舍去)?
将p=![]() 代入⑤得m2=
代入⑤得m2=![]() ,所以m=
,所以m=![]() 或m=-
或m=-![]() ,?
,?
由上知,满足条件的m、p存在,且m=![]() 或m=-
或m=-![]() .p=
.p=![]() .
.
点评:本题主要考查了椭圆、双曲线、直线与圆锥曲线的位置关系等知识,考查运算、综合分析和解决问题的能力.

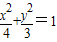 ,抛物线C2:(y-m)2=2px(p>0),且C1、C2的公共弦AB过椭圆C1的右焦点.
,抛物线C2:(y-m)2=2px(p>0),且C1、C2的公共弦AB过椭圆C1的右焦点.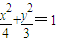 ,抛物线C2:(y-m)2=2px(p>0),且C1、C2的公共弦AB过椭圆C1的右焦点.
,抛物线C2:(y-m)2=2px(p>0),且C1、C2的公共弦AB过椭圆C1的右焦点.