题目内容
已知椭圆C1: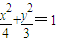 ,抛物线C2:(y-m)2=2px(p>0),且C1、C2的公共弦AB过椭圆C1的右焦点.
,抛物线C2:(y-m)2=2px(p>0),且C1、C2的公共弦AB过椭圆C1的右焦点.(Ⅰ)当AB⊥x轴时,求m、p的值,并判断抛物线C2的焦点是否在直线AB上;
(Ⅱ)是否存在m、p的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的m、p的值;若不存在,请说明理由.
【答案】分析:(Ⅰ)由题意知当AB⊥x轴时,直线AB的方程为:x=1,从而点A的坐标为(1, )或(1,-
)或(1,- ).因为点A在抛物线上.
).因为点A在抛物线上.
所以 ,即
,即 .此时C2的焦点坐标为(
.此时C2的焦点坐标为( ,0),该焦点不在直线AB上.
,0),该焦点不在直线AB上.
(II)解法一:假设存在m、p的值使C2的焦点恰在直线AB上,由(I)知直线AB的斜率存在,故可设直线AB的方程为y=k(x-1).由 消去y得(3+4k2)x2-8k2x+4k2-12=0.设A、B的坐标分别为(x1,y1),(x2,y2),由根与系数的关系可推导出求出符合条件的m、p的值.
消去y得(3+4k2)x2-8k2x+4k2-12=0.设A、B的坐标分别为(x1,y1),(x2,y2),由根与系数的关系可推导出求出符合条件的m、p的值.
解法二:设A、B的坐标分别为(x1,y1),(x2y2).因为AB既过C1的右焦点F(1,0),又过C2的焦点 ,所以
,所以 . 由(Ⅰ)知x1≠x2,p≠2,于是直线AB的斜率
. 由(Ⅰ)知x1≠x2,p≠2,于是直线AB的斜率 .且直线AB的方程是
.且直线AB的方程是 .由此入手可求出符合条件的m、p的值.
.由此入手可求出符合条件的m、p的值.
解答: 解:(Ⅰ)当AB⊥x轴时,点A、B关于x轴对称,所以m=0,直线AB的方程为:
解:(Ⅰ)当AB⊥x轴时,点A、B关于x轴对称,所以m=0,直线AB的方程为:
x=1,从而点A的坐标为(1, )或(1,-
)或(1,- ).
).
因为点A在抛物线上.
所以 ,即
,即 .
.
此时C2的焦点坐标为( ,0),该焦点不在直线AB上.
,0),该焦点不在直线AB上.
(II)解法一:假设存在m、p的值使C2的焦点恰在直线AB上,由(I)知直线AB
的斜率存在,故可设直线AB的方程为y=k(x-1).
由 消去y得(3+4k2)x2-8k4x+4k2-12=0①
消去y得(3+4k2)x2-8k4x+4k2-12=0①
设A、B的坐标分别为(x1,y1),(x2,y2),
则x1,x2是方程①的两根,x1+x2= .
.
由
消去y得(kx-k-m)2=2px.②
因为C2的焦点 在直线y=k(x-1)上,
在直线y=k(x-1)上,
所以 ,即
,即 .代入②有
.代入②有 .
.
即 .=3 ③
.=3 ③
由于x1,x2也是方程=3 ③的两根,
所以x1+x2= .
.
从而 =
= .
.
解得 =4 ④
=4 ④
又AB过C1…C2的焦点,
所以 ,
,
则 .=5 ⑤
.=5 ⑤
由=4 ④、=5 ⑤式得 ,即k4-5k2-6=0.
,即k4-5k2-6=0.
解得k2=6.于是 .
.
因为C2的焦点 在直线
在直线 上,
上,
所以 .
.
∴ 或
或 .
.
由上知,满足条件的m、p存在,且 或
或 ,
, .
.
解法二:设A、B的坐标分别为(x1,y1),(x2y2).
因为AB既过C1的右焦点F(1,0),又过C2的焦点 ,
,
所以 .
.
即 . ①
. ①
由(Ⅰ)知x1≠x2,p≠2,于是直线AB的斜率 ,②
,②
且直线AB的方程是 ,
,
所以 .③
.③
又因为 ,
,
所以 .④
.④
将①、②、③代入④得 .=5 ⑤
.=5 ⑤
因为 ,
,
所以 .=6 ⑥
.=6 ⑥
将②、③代入=6 ⑥得 .=7 ⑦
.=7 ⑦
由=5 ⑤、=7 ⑦得 =
= .
.
即3p2+20p-32=0
解得 .
.
将 代入=5 ⑤得
代入=5 ⑤得 ,
,
∴ 或
或 .
.
由上知,满足条件的m、p存在,
且 或
或 ,
,
点评:本题考查直线和圆锥轴线的位置关系和综合运用,解题时要认真审题,仔细解答,注意公式的灵活运用.
 )或(1,-
)或(1,- ).因为点A在抛物线上.
).因为点A在抛物线上.所以
 ,即
,即 .此时C2的焦点坐标为(
.此时C2的焦点坐标为( ,0),该焦点不在直线AB上.
,0),该焦点不在直线AB上.(II)解法一:假设存在m、p的值使C2的焦点恰在直线AB上,由(I)知直线AB的斜率存在,故可设直线AB的方程为y=k(x-1).由
 消去y得(3+4k2)x2-8k2x+4k2-12=0.设A、B的坐标分别为(x1,y1),(x2,y2),由根与系数的关系可推导出求出符合条件的m、p的值.
消去y得(3+4k2)x2-8k2x+4k2-12=0.设A、B的坐标分别为(x1,y1),(x2,y2),由根与系数的关系可推导出求出符合条件的m、p的值.解法二:设A、B的坐标分别为(x1,y1),(x2y2).因为AB既过C1的右焦点F(1,0),又过C2的焦点
 ,所以
,所以 . 由(Ⅰ)知x1≠x2,p≠2,于是直线AB的斜率
. 由(Ⅰ)知x1≠x2,p≠2,于是直线AB的斜率 .且直线AB的方程是
.且直线AB的方程是 .由此入手可求出符合条件的m、p的值.
.由此入手可求出符合条件的m、p的值.解答:
 解:(Ⅰ)当AB⊥x轴时,点A、B关于x轴对称,所以m=0,直线AB的方程为:
解:(Ⅰ)当AB⊥x轴时,点A、B关于x轴对称,所以m=0,直线AB的方程为:x=1,从而点A的坐标为(1,
 )或(1,-
)或(1,- ).
).因为点A在抛物线上.
所以
 ,即
,即 .
.此时C2的焦点坐标为(
 ,0),该焦点不在直线AB上.
,0),该焦点不在直线AB上.(II)解法一:假设存在m、p的值使C2的焦点恰在直线AB上,由(I)知直线AB
的斜率存在,故可设直线AB的方程为y=k(x-1).
由
 消去y得(3+4k2)x2-8k4x+4k2-12=0①
消去y得(3+4k2)x2-8k4x+4k2-12=0①设A、B的坐标分别为(x1,y1),(x2,y2),
则x1,x2是方程①的两根,x1+x2=
 .
.由

消去y得(kx-k-m)2=2px.②
因为C2的焦点
 在直线y=k(x-1)上,
在直线y=k(x-1)上,所以
 ,即
,即 .代入②有
.代入②有 .
.即
 .=3 ③
.=3 ③由于x1,x2也是方程=3 ③的两根,
所以x1+x2=
 .
.从而
 =
= .
.解得
 =4 ④
=4 ④又AB过C1…C2的焦点,
所以
 ,
,则
 .=5 ⑤
.=5 ⑤由=4 ④、=5 ⑤式得
 ,即k4-5k2-6=0.
,即k4-5k2-6=0.解得k2=6.于是
 .
.因为C2的焦点
 在直线
在直线 上,
上,所以
 .
.∴
 或
或 .
.由上知,满足条件的m、p存在,且
 或
或 ,
, .
.解法二:设A、B的坐标分别为(x1,y1),(x2y2).
因为AB既过C1的右焦点F(1,0),又过C2的焦点
 ,
,所以
 .
.即
 . ①
. ①由(Ⅰ)知x1≠x2,p≠2,于是直线AB的斜率
 ,②
,②且直线AB的方程是
 ,
,所以
 .③
.③又因为
 ,
,所以
 .④
.④将①、②、③代入④得
 .=5 ⑤
.=5 ⑤因为
 ,
,所以
 .=6 ⑥
.=6 ⑥将②、③代入=6 ⑥得
 .=7 ⑦
.=7 ⑦由=5 ⑤、=7 ⑦得
 =
= .
.即3p2+20p-32=0
解得
 .
.将
 代入=5 ⑤得
代入=5 ⑤得 ,
,∴
 或
或 .
.由上知,满足条件的m、p存在,
且
 或
或 ,
,
点评:本题考查直线和圆锥轴线的位置关系和综合运用,解题时要认真审题,仔细解答,注意公式的灵活运用.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
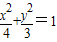 ,抛物线C2:(y-m)2=2px(p>0),且C1、C2的公共弦AB过椭圆C1的右焦点.
,抛物线C2:(y-m)2=2px(p>0),且C1、C2的公共弦AB过椭圆C1的右焦点.