题目内容
如图,在三棱锥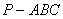 中,直线
中,直线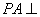 平面
平面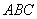 ,且
,且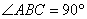 ,又点
,又点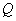 ,
,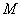 ,
,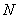 分别是线段
分别是线段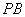 ,
,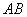 ,
,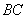 的中点,且点
的中点,且点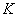 是线段
是线段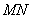 上的动点.
上的动点.
(1)证明:直线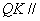 平面
平面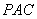 ;
;
(2) 若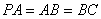 ,求二面角
,求二面角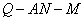 的平面角的余弦值。
的平面角的余弦值。
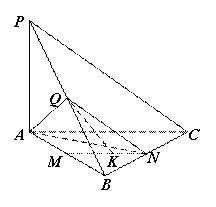
(1).连结QM 因为点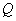 ,
,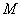 ,
,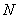 分别是线段
分别是线段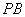 ,
,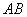 ,
,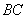 的中点
的中点
所以QM∥PA MN∥AC QM∥平面PAC MN∥平面PAC
因为MN∩QM=M 所以平面QMN∥平面PAC QK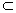 平面QMN
平面QMN
所以QK∥平面PAC
(2)方法1:过M作MH⊥AN于H,连QH,则∠QHM即为
二面角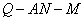 的平面角, 令
的平面角, 令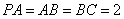 -
-
即QM=AM=1所以
此时sin∠MAH=sin∠BAN=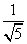 MH=
MH=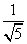 记二面角
记二面角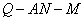 的平面角为
的平面角为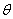
则tan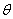 =
=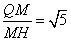 COS
COS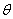 =
=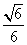 即为所求。 方法2:以B为原点,以BC、BA所在直线为x轴y轴建空间直角坐标系,设
即为所求。 方法2:以B为原点,以BC、BA所在直线为x轴y轴建空间直角坐标系,设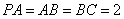
则A(0,2,0),M(0,1,0),N(1,0,0),p(0,2,2),Q(0,1,1),
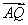 =(0,-1,1),
=(0,-1,1), 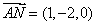 -
-
记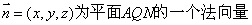 ,则
,则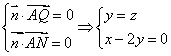
取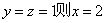
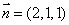 -
-
又平面ANM的一个法向量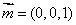 ,所以cos
,所以cos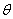 =
=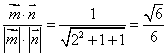
即为所求。

练习册系列答案
相关题目
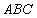 的中线
的中线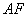 与中位线
与中位线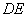 相交于
相交于 ,已知
,已知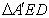 是△
是△ 绕
绕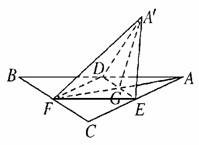 A.动点
A.动点 在平面
在平面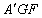 ⊥平面
⊥平面
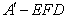 的体积有最大值
的体积有最大值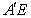 与
与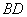 不可能垂直
不可能垂直 ,
, ,求异面直线
,求异面直线 所成角的余弦值为
所成角的余弦值为  的前
的前 项和为
项和为 ,若
,若 ,则下列式子中数值不能确定的是:
,则下列式子中数值不能确定的是:  .
.
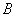 .
. 
 .
.
 .
.
 的两个焦点为
的两个焦点为 ,点
,点 在椭圆上,若
在椭圆上,若 ,则
,则
 .
.
