题目内容
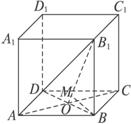
已知正四棱柱ABCD—A1B1C1D1的底面边长为2,侧棱长为
.(1)求二面角B1—AC—B的大小;
(2)求点B到平面AB1C的距离.
解析:(1)连结AC、BD交于点O,连结B1O,易知BB1⊥底面ABCD且BO⊥AC,∴B1O⊥AC.
∴∠B1OB是二面角B1ACB的平面角.
在Rt△B1BO中,B1B=
,OB=
×2=
.
∴tan∠B1OB=1,且∠B1OB为锐角.
∴∠B1OB=45°,即二面角B1ACB为45°.
(2)作BM⊥B1O于M,由AC⊥平面B1OB,∴BM⊥AC.
∴BM⊥平面AB1C,即BM为点B到平面AB1C的距离.
在等腰Rt△B1BO中,BB1=
,OB=
,∴BM=1.
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
如图所示，已知正四棱柱ABCD-A1B1C1D1的底面边长为1，点E在棱AA1上，A1C∥平面EBD，截面EBD的面积为
如图，已知正四棱柱ABCD-A1B1C1D1与它的侧视图（或称左视图），E是DD1上一点，AE⊥B1C．
（2006•广州模拟）已知正四棱柱ABCD-A1B1C1D1，AB=BC=1，AA1=2，点E为CC1的中点，点F为BD1的中点．