题目内容
已知等比数列{an}的首项为1,公比q≠1,Sn为其前n项和,a1,a2,a3分别为某等差数列的第一、第二、第四项.
(1)求an和Sn.
(2)设 ,数列
,数列 的前n项和为Tn,求证:
的前n项和为Tn,求证:
解:(1)因为a1,a2,a3为某等差数列的第一、第二、第四项,
所以a3-a2=2(a2-a1),
所以a1q2-a1q=2(a1q-a1),
因为a1=1,所以q2-3q+2=0,
因为q≠1,所以q=2,
所以an=a1qn-1=2n-1,
 ……………6分
……………6分
(2)由(1)知an+1=2n,
所以bn=log2an+1=log22n=n.
所以 .
.

 。……………12分
。……………12分

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
从某大学中随机抽取8名女大学生, 其身高和体重数据如表所示.
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 身高/cm | 165 | 165 | 157 | 170 | 175 | 165 | 155 | 170 |
| 体重/kg | 48 | 57 | 50 | 54 | 64 | 61 | 43 | 59 |
已知该大学某女大学生身高为165.25cm, 则预报其体重合理值为 kg.
 在区间[-2,2]上的值域是_
在区间[-2,2]上的值域是_  满足条件
满足条件 ,当且仅当
,当且仅当 时,
时, 取最小值,则实数
取最小值,则实数 的取值范围是
的取值范围是 B.
B. C.
C. D.
D.
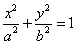 ,双曲线 C2 的方程为
,双曲线 C2 的方程为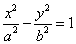 ,C1 与 C2 的离心率之积为
,C1 与 C2 的离心率之积为 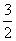 , 则 C1 、 C2 的离心率分别为
, 则 C1 、 C2 的离心率分别为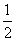 ,3 B.
,3 B.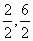 C.
C.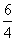 ,2 D.
,2 D.
 , 则z = m a x{2x + 3y - 1 , x + 2y + 2} 的取值范围是
, 则z = m a x{2x + 3y - 1 , x + 2y + 2} 的取值范围是 B.
B. 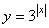 C.
C.  D.
D. 
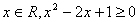 ”的否定是( )
”的否定是( )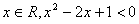 D 对任意的
D 对任意的