��Ŀ����
ij��˾Ϊ��������26.8��Ԫ��Ϣ����û�г����IJм����̵꣬���20��Ԫ�����̵�Ľ��ɾ�Ӫ״�����õ�ij������Ʒר���꣬��Լ���øõ꾭Ӫ����������ծ������ծ���������Ϣ������֪��������Ʒ�Ľ���Ϊÿ��40Ԫ���õ�ÿ��������q���ټ��������ۼ�p��Ԫ/����֮��Ĺ�ϵ����ͼ�е�һ�����ߣ�ʵ�ߣ���ʾ��ְ��ÿ��ÿ�¹���Ϊ1200Ԫ���õ�Ӧ��������������Ϊÿ��13200Ԫ��
��1���������ۼ�pΪ52Ԫ/��ʱ���õ�������֧ƽ�⣬��õ��ְ��������
��2�����õ�ֻ����20��ְ������õ�������ڼ����������ծ��ʱÿ������Ʒ�ļ۸�Ϊ����Ԫ��
��1���������ۼ�pΪ52Ԫ/��ʱ���õ�������֧ƽ�⣬��õ��ְ��������
��2�����õ�ֻ����20��ְ������õ�������ڼ����������ծ��ʱÿ������Ʒ�ļ۸�Ϊ����Ԫ��

�⣺������õ��������ΪSԪ����ְ��m����
��S=q��p��40����100��1200m��13200��
����ͼ��֪��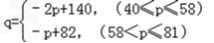 ��
��
����S=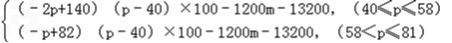 ��
��
����֪����p=52 ʱ��S=0����������2p+140����p��40����100��1200m��13200=0��
���m=25������ʱ�õ���25��ְ����
�������õ�ֻ����20��ְ������������
S=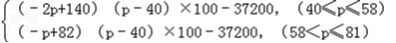 ��
��
��40��p��58 ʱ����� p=55ʱ��Sȡ���ֵ7800Ԫ��
��58��p��81 ʱ����� p=61ʱ��Sȡ���ֵ6900Ԫ��
���ϣ���p=55 ʱ��S�����ֵ7800Ԫ��
��õ��������n�����ծ��
�����⣬��12n��7800��268000��200000��0�����n��5��
���ԣ��õ��������5�����ծ��ʱ����Ʒ�ĵ��۶�Ϊ55Ԫ��
��S=q��p��40����100��1200m��13200��
����ͼ��֪��
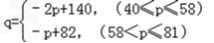 ��
������S=
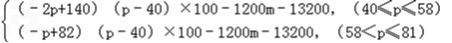 ��
������֪����p=52 ʱ��S=0����������2p+140����p��40����100��1200m��13200=0��
���m=25������ʱ�õ���25��ְ����
�������õ�ֻ����20��ְ������������
S=
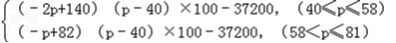 ��
����40��p��58 ʱ����� p=55ʱ��Sȡ���ֵ7800Ԫ��
��58��p��81 ʱ����� p=61ʱ��Sȡ���ֵ6900Ԫ��
���ϣ���p=55 ʱ��S�����ֵ7800Ԫ��
��õ��������n�����ծ��
�����⣬��12n��7800��268000��200000��0�����n��5��
���ԣ��õ��������5�����ծ��ʱ����Ʒ�ĵ��۶�Ϊ55Ԫ��

��ϰ��ϵ�д�
�����Ŀ
 ij��˾Ϊ��������26.8��Ԫ��Ϣ����û�г����IJм����̵꣬���20��Ԫ�����̵�Ľ��ɾ�Ӫ״�����õ�ij������Ʒר���꣬��Լ���øõ꾭Ӫ����������ծ������ծ���������Ϣ������֪��������Ʒ�Ľ���Ϊÿ��40Ԫ���õ�ÿ��������q���ټ��������ۼ�p��Ԫ/����֮��Ĺ�ϵ����ͼ�е�һ�����ߣ�ʵ�ߣ���ʾ��ְ��ÿ��ÿ�¹���Ϊ1200Ԫ���õ�Ӧ��������������Ϊÿ��13200Ԫ��
ij��˾Ϊ��������26.8��Ԫ��Ϣ����û�г����IJм����̵꣬���20��Ԫ�����̵�Ľ��ɾ�Ӫ״�����õ�ij������Ʒר���꣬��Լ���øõ꾭Ӫ����������ծ������ծ���������Ϣ������֪��������Ʒ�Ľ���Ϊÿ��40Ԫ���õ�ÿ��������q���ټ��������ۼ�p��Ԫ/����֮��Ĺ�ϵ����ͼ�е�һ�����ߣ�ʵ�ߣ���ʾ��ְ��ÿ��ÿ�¹���Ϊ1200Ԫ���õ�Ӧ��������������Ϊÿ��13200Ԫ�� ij��˾Ϊ��������26.8��Ԫ��Ϣ����û�г����IJм����̵꣬���20��Ԫ�����̵�Ľ��ɾ�Ӫ״�����õ�ij������Ʒר���꣬��Լ���øõ꾭Ӫ����������ծ������ծ���������Ϣ����
ij��˾Ϊ��������26.8��Ԫ��Ϣ����û�г����IJм����̵꣬���20��Ԫ�����̵�Ľ��ɾ�Ӫ״�����õ�ij������Ʒר���꣬��Լ���øõ꾭Ӫ����������ծ������ծ���������Ϣ����
 ij��˾Ϊ��������26.8��Ԫ��Ϣ����û�г����IJм����̵꣬���20��Ԫ�����̵�Ľ��ɾ�Ӫ״�����õ�ij������Ʒר���꣬��Լ���øõ꾭Ӫ����������ծ������ծ���������Ϣ������֪��������Ʒ�Ľ���Ϊÿ��40Ԫ���õ�ÿ��������q���ټ��������ۼ�p��Ԫ/����֮��Ĺ�ϵ����ͼ�е�һ�����ߣ�ʵ�ߣ���ʾ��ְ��ÿ��ÿ�¹���Ϊ1200Ԫ���õ�Ӧ��������������Ϊÿ��13200Ԫ��
ij��˾Ϊ��������26.8��Ԫ��Ϣ����û�г����IJм����̵꣬���20��Ԫ�����̵�Ľ��ɾ�Ӫ״�����õ�ij������Ʒר���꣬��Լ���øõ꾭Ӫ����������ծ������ծ���������Ϣ������֪��������Ʒ�Ľ���Ϊÿ��40Ԫ���õ�ÿ��������q���ټ��������ۼ�p��Ԫ/����֮��Ĺ�ϵ����ͼ�е�һ�����ߣ�ʵ�ߣ���ʾ��ְ��ÿ��ÿ�¹���Ϊ1200Ԫ���õ�Ӧ��������������Ϊÿ��13200Ԫ�� ij��˾Ϊ��������26.8��Ԫ��Ϣ����û�г����IJм����̵꣬���20��Ԫ�����̵�Ľ��ɾ�Ӫ״�����õ�ij������Ʒר���꣬��Լ���øõ꾭Ӫ����������ծ������ծ���������Ϣ������֪��������Ʒ�Ľ���Ϊÿ��40Ԫ���õ�ÿ��������q���ټ��������ۼ�p��Ԫ/����֮��Ĺ�ϵ����ͼ�е�һ�����ߣ�ʵ�ߣ���ʾ��ְ��ÿ��ÿ�¹���Ϊ1200Ԫ���õ�Ӧ��������������Ϊÿ��13200Ԫ��
ij��˾Ϊ��������26.8��Ԫ��Ϣ����û�г����IJм����̵꣬���20��Ԫ�����̵�Ľ��ɾ�Ӫ״�����õ�ij������Ʒר���꣬��Լ���øõ꾭Ӫ����������ծ������ծ���������Ϣ������֪��������Ʒ�Ľ���Ϊÿ��40Ԫ���õ�ÿ��������q���ټ��������ۼ�p��Ԫ/����֮��Ĺ�ϵ����ͼ�е�һ�����ߣ�ʵ�ߣ���ʾ��ְ��ÿ��ÿ�¹���Ϊ1200Ԫ���õ�Ӧ��������������Ϊÿ��13200Ԫ��