题目内容
某企业有甲、乙两个研发小组,他们研发新产品成功的概率分别为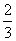 和
和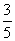 ,现安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立.
,现安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立.
(1)求至少有一种新产品研发成功的概率;
(2)若新产品A研发成功,预计企业可获利润120万元;若新产品B研发成功,预计企业可获利润100万元,求该企业可获利润的分布列和数学期望.
解:(1)设至少有一组研发成功的事件为事件A且事件B为事件A的对立事件,则事件B为一种新产品都没有成功,因为甲,乙成功的概率分别为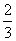 ,
,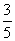 .
.
则P(B)=(1-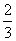 )×(1-
)×(1-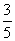 )=
)= ×
× =
= ,
,
再根据对立事件概率之间的公式可得
P(A)=1-P(B)= ,
,
所以至少一种产品研发成功的概率为 .
.
(2)由题可设该企业可获得利润为ξ,则ξ的取值有0,120+0,100+0,120+100,即ξ=0,120,100,220,由独立试验的概率计算公式可得:
P(ξ=0)=(1-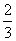 )×(1-
)×(1-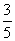 )=
)= ;
;
P(ξ=120)=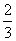 ×(1-
×(1-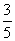 )=
)= ;
;
P(ξ=100)=(1-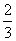 )×
)×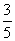 =
= ;
;
P(ξ=220)=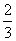 ×
×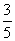 =
= ;
;
所以ξ的分布列如下:
| ξ | 0 | 120 | 100 | 220 |
| P(ξ) |
|
|
|
|

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 B. 16
B. 16 C. 9
C. 9
 是指数函数,则
是指数函数,则 的值是______________.
的值是______________. 与时间
与时间 (月)的关系:
(月)的关系: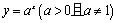 ,有以下叙述:
,有以下叙述: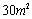 ;
;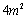 蔓延到
蔓延到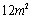 需要经过
需要经过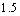 个月;
个月;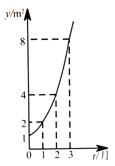
 的递减区间为 ………………………………………………( )
的递减区间为 ………………………………………………( ) )
) (
( )
) (
( )
) (
( )
)
 的复数
的复数 为______________
为______________