题目内容
已知 ,则函数
,则函数 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
C
解析试题分析:由于 ,则
,则 ,所以
,所以 ,当且仅当
,当且仅当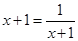 ,由于
,由于 ,即当
,即当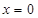 时,上式取等号,因此函数
时,上式取等号,因此函数 的最小值为
的最小值为 ,故选C.
,故选C.
考点:基本不等式

练习册系列答案
相关题目
对任意正数x,y不等式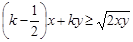 恒成立,则实数
恒成立,则实数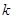 的最小值是 ( )
的最小值是 ( )
| A.1 | B.2 | C.3 | D.4 |
设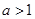 ,
,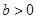 ,若
,若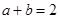 ,则
,则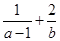 的最小值为( )
的最小值为( )
A.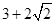 | B.6 | C.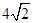 | D.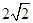 |
设第一象限内的点 满足约束条件
满足约束条件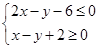 ,若目标函数
,若目标函数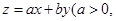
 的最大值为40,则
的最大值为40,则 的最小值为( )
的最小值为( )
A. | B. | C.1 | D.4 |
若正数 满足
满足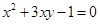 ,则
,则 的最小值是( )
的最小值是( )
A. | B. | C.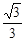 | D. |
某车间分批生产某种产品,每批的生产准备费用为800元.若每批生产x件,则平均仓储时间为 天,且每件产品每天的仓储费用为1元.为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品( )
天,且每件产品每天的仓储费用为1元.为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品( )
| A.60件 | B.80件 |
| C.100件 | D.120件 |
已知矩形ABCD的面积为8,当矩形ABCD周长最小时,沿对角线AC把
△ACD折起,则三棱锥D-ABC外接的球表面积等于( ).
| A.8π | B.16π | C.48 π π | D.不确定的实数 |
若a,b∈R,且ab>0,则下列不等式中,恒成立的是( )
A.a+b≥2  | B.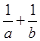 > > | C.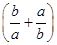 ≥2 ≥2 | D.a2+b2>2ab |
已知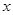 ,
, ,且
,且 ,则
,则 的最大值是( )
的最大值是( )
| A.3 | B.3.5 | C.4 | D.4.5 |