题目内容
7.已知F1、F2分别是椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点,点P在椭圆C上,线段PF1的中点在y轴上,若2∠PF1F2=∠F1PF2,那么椭圆的离心率为$\frac{\sqrt{5}-1}{2}$.分析 由题意画出图形,结合三角形中位线定理可知PF2⊥x轴,又2∠PF1F2=∠F1PF2,则∠PF1F2=30°,再求解直角三角形可得椭圆的离心率.
解答 解:如图,
设线段PF1的中点为M,则OM∥PF2,
∴PF2⊥x轴,
又2∠PF1F2=∠F1PF2,则∠PF1F2=30°,
∴sin30°=$\frac{P{F}_{2}}{{F}_{1}{F}_{2}}=\frac{\frac{{b}^{2}}{a}}{2c}=\frac{1}{2}$,得$e=\frac{c}{a}=\frac{\sqrt{5}-1}{2}$.
故答案为:$\frac{\sqrt{5}-1}{2}$.
点评 本题考查椭圆的简单性质,考查了数学转化思想方法和数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
18.椭圆16x2+25y2=400的长轴长为( )
| A. | 5 | B. | 10 | C. | 25 | D. | 50 |
2.设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(-2)=0,当x>0时,xf′(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是( )
| A. | (-∞,-2)∪(0,2) | B. | (-∞,-2)∪(2,+∞) | C. | (-2,0)∪(2,+∞) | D. | (-2,0)∪(0,2) |
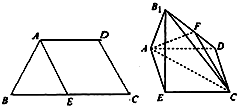 如图,已知四边形ABCD满足AD∥BC,AB=AD=CD=$\frac{1}{2}$BC=2,E是BC的中点,将△BAE沿AE折成△B1AE,使面B1AE⊥面AECD,F为棱B1D上一点.
如图,已知四边形ABCD满足AD∥BC,AB=AD=CD=$\frac{1}{2}$BC=2,E是BC的中点,将△BAE沿AE折成△B1AE,使面B1AE⊥面AECD,F为棱B1D上一点.