题目内容

已知
OA
=
a
，
OB
=
b
，|
a
|=2，|
b
|=3，任意点M关于点A的对称点为S，点S关于点B的对称点为N，点C为线段AB中点，则
MN
•
OC
=
5
5
．
分析：由题意可得，
MN
=2
AB
=2（
OB
-
OA
），
OC
=
1
2
（
OB
+
OA
），再由 
MN
•
OC
=2（
OB
-
OA
）•
1
2
（
OB
+
OA
）=
OB
2-
OA
2，运算求得结果．
解答：解：由题意可得，AB是△SMN的中位线，∴
MN
=2
AB
=2（
OB
-
OA
）．
再由点C为线段AB中点，可得
OC
=
1
2
（
OB
+
OA
），
∴
MN
•
OC
=2（
OB
-
OA
）•
1
2
（
OB
+
OA
）=
OB
2-
OA
2=9-4=5，
故答案为 5．
点评：本题主要考查两个向量的数量积的运算，两个向量的加减法的法则，以及其几何意义，属于中档题．
练习册系列答案
相关题目
已知
OA
=
a
，
OB
=
b
，
a
•
b
=|
a
-
b
|=2，
（1）当△AOB的面积最大时，求
a
与
b
的夹角θ；
（2）在（1）的条件下，判断△AOB的形状，并说明理由．
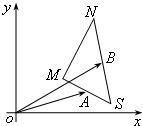精英家教网如图，已知
OA
=
a
，
OB
=
b
，对任意点M，M点关于A点的对称点为S，S点关于B点的对称点为N，用
a
、
b
表示向量
MN
．
（1）已知数列{an}的前几项和为sn=
3
2
(an-1)(n∈N*)
①求数列的通项公式；
②求数列{an}的前n项和．
（2）已知
OA
=
a
，
OB
=
b
，且|
a
|=|
b
|=4，∠AOB=60°，
①求|
a
+
b
|，|
a
-
b
|； 
②求（
a
+
b
）与
a
的夹角．
已知
OA
=
a
，
OB
=
b
，
OC
=
c
，
OD
=
d
，
OE
=
e
，且向量
a
与向量
b
为不共线的两个向量，设
c
=3
a
，
d
=2
b
，
e
=t（
a
+
b
），t为实数．
（1）用向量
a
，
b
或实数t来表示向量
CD
，
CE
；
（2）实数t为何值时，C，D，E三点在一条直线上？
已知
OA
=
a
，
OB
=
b
，且|
a
|=|
b
|=4，∠AOB=60°，则
a
+
b
与
a
的夹角是
 
；
a
-
b
与
a
的夹角是
 
；△AOB的面积是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网