题目内容
已知 .
.
(1)求f(x)的定义域;
(2)求f(x)的最大值和最小值;
(3)若 ,如何由(2)的结论求g(x)的最大值和最小值.
,如何由(2)的结论求g(x)的最大值和最小值.
解:(1)f(x)的定义域为[0,1].
(2) ,
,
设 ,∴
,∴ ,
,
则 ,
,
当α=β时, ,此时f(x)最大值为
,此时f(x)最大值为 ,
,
又cos(β-α)在 递增,在
递增,在 递减,
递减,
∴f(x)的最小值是f(0)与f(1)的较小者,即A与B的较小者.
(3)设 ,∴
,∴ ,
,
则 ,
,
由(2)知g(x)的最大值为 ,
,
最小值为 和
和 的较小者,即
的较小者,即 .
.
分析:(1)根据要使偶次根式有意义,只需根式里大于等于零,建立不等关系,解之即可;
(2)利用三角换元,转化成 ,然后研究cos(β-α)在[0,1]上的单调性,求出最值即可;
,然后研究cos(β-α)在[0,1]上的单调性,求出最值即可;
(3)设 ,
, ,将
,将 转化成
转化成 ,利用上一问结论即可求得最值.
,利用上一问结论即可求得最值.
点评:本题主要考查了函数的定义域及其求法,以及函数的最值及其几何意义,属于基础题.
(2)
 ,
,设
 ,∴
,∴ ,
,则
 ,
,当α=β时,
 ,此时f(x)最大值为
,此时f(x)最大值为 ,
,又cos(β-α)在
 递增,在
递增,在 递减,
递减,∴f(x)的最小值是f(0)与f(1)的较小者,即A与B的较小者.
(3)设
 ,∴
,∴ ,
,则
 ,
,由(2)知g(x)的最大值为
 ,
,最小值为
 和
和 的较小者,即
的较小者,即 .
.分析:(1)根据要使偶次根式有意义,只需根式里大于等于零,建立不等关系,解之即可;
(2)利用三角换元,转化成
 ,然后研究cos(β-α)在[0,1]上的单调性,求出最值即可;
,然后研究cos(β-α)在[0,1]上的单调性,求出最值即可;(3)设
 ,
, ,将
,将 转化成
转化成 ,利用上一问结论即可求得最值.
,利用上一问结论即可求得最值.点评:本题主要考查了函数的定义域及其求法,以及函数的最值及其几何意义,属于基础题.

练习册系列答案
相关题目
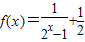
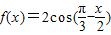
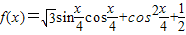 .
.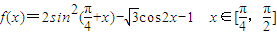
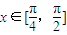 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.