题目内容
用数学归纳法证明:(n+1)+ (n+2)+…+(n+n)=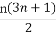
(n∈N*)的第二步中,当n=k+1时等式左边与n=k时的等式左边的差等于 .
3k+2
【解析】n=k+1比n=k时左边变化的项为(2k+1)+(2k+2)-(k+1)=3k+2.
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
用数学归纳法证明:(n+1)+ (n+2)+…+(n+n)=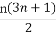(n∈N*)的第二步中,当n=k+1时等式左边与n=k时的等式左边的差等于 .
3k+2
【解析】n=k+1比n=k时左边变化的项为(2k+1)+(2k+2)-(k+1)=3k+2.
阅读快车系列答案
