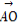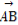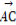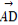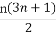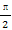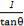题目内容
设函数f(x)满足2f(x)-f(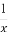 )=4x-
)=4x- +1,数列{an}和{bn}满足下列条件:a1=1,an+1-2an=f(n),bn=an+1-an(n∈N*).
+1,数列{an}和{bn}满足下列条件:a1=1,an+1-2an=f(n),bn=an+1-an(n∈N*).
(1)求f(x)的解析式.
(2)求{bn}的通项公式bn.
(3)试比较2an与bn的大小,并证明你的结论.
(1) f(x)=2x+1 (2) bn=3·2n-2 (3)见解析
【解析】(1)∵2f(x)-f( )=4x-
)=4x-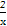 +1,
+1,
∴2f( )-f(x)=
)-f(x)=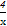 -2x+1.
-2x+1.
联立方程组
①×2+②,得3f(x)=6x+3
∴f(x)=2x+1.
(2)由题设an+1=2an+2n+1 ③,
an+2=2an+1+2n+3 ④,
④-③得an+2-an+1=2(an+1-an)+2,
即bn+1=2bn+2,∴bn+1+2=2(bn+2),
∴{bn+2}为等比数列.
q=2,b1=a2-a1=4,bn+2=6·2n-1,
∴bn=3·2n-2.
(3)由(2),知an+1-an=3×2n-2,而已知an+1-2an=2n+1,联立解得an=3×2n-2n-3,
∴2an=6×2n-4n-6,
∴2an-bn=3×2n-4(n+1).
当n=1时,2a1-b1=-2<0,∴2a1<b1;
当n=2时,2a2-b2=0,∴2a2=b2;
当n=3时,2a3-b3=8>0,∴2a3>b3;
当n=4时,2a4-b4=28>0,∴2a4>b4.
猜想当n≥3时,2an>bn即3×2n>4(n+1).
当n=3时,显然成立,
假设当n=k(k≥3)时,命题正确,
即3×2k>4(k+1).
当n=k+1时,
即3×2k+1=2×(3×2k)>8(k+1)=8k+8
=4k+8+4k>4k+8=4(k+2).
不等式也成立,故对一切n≥3且n∈N*,
2an>bn.
综上所述,当n=1时,2an<bn;
当n=2时,2an=bn;
当n≥3时,2an>bn.