题目内容
如图，已知抛物线
的准线为l，在l上任取一点M，过M作抛物线的切线MA、MB，A、B为切点．
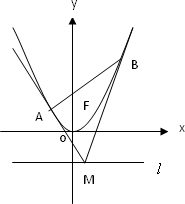
(Ⅰ)求弦长|AB|的取值范围；
(Ⅱ)求证：直线AB恒过抛物线的焦点F；
(Ⅲ)试判断以AB为直径的端点的圆与原点O的位置关系，并说明理由．
答案：
解析：
解析：
|
解：(Ⅰ) ∴MA的方程为 ∴ ∴ (Ⅱ)AB的方程为 ∴直线AB恒过抛物线的焦点F(0，1)． (Ⅲ) ∴原点O在以AB为直径端点的圆的内部． |
，即
．
，也即
，同理
为方程
的两根．
，
＝
＝
的取值范围是
，即
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
（2013•浙江模拟）如图，已知抛物线的方程为x2=2py（p＞0），过点A（0，-1）作直线与抛物线相交于P，Q两点，点B的坐标为（0，1），连接BP，BQ，设QB，BP与x轴分别相交于M，N两点．如果QB的斜率与PB的斜率的乘积为-3，则∠MBN的大小等于（ ）
的焦点为
，
是抛物线上横坐标为8且位于
轴上方的点. 
垂直于
轴，垂足为
，
的中点为
（
为坐标原点）. 
的方程；
，垂足为
，求点
是
与圆
的准线为
，
为
的两条切线，切点分别为
，
，再分别过
，
．求证：直线
必经过
轴上的一个定点
，并写出点