题目内容
如图，已知抛物线
的准线为
，
为上的一个动点，过点作抛物线
的两条切线，切点分别为
，
，再分别过，两点作的垂线，垂足分别为
，
．求证：直线
必经过
轴上的一个定点
，并写出点的坐标.
解：因为抛物线的准线
的方程为
，所以可设点
的坐标分别为
，
，
，则
，
， 由
，得
，求导数得
，于是
，即
，
化简得
，
同理可得
，
所以
和
是关于
的方程
两个实数根，所以
，且
．
在直线
的方程
中，
令
，
得
=
为定值，
所以直线必经过
轴上的一个定点
，即抛物线的焦点．
练习册系列答案
相关题目
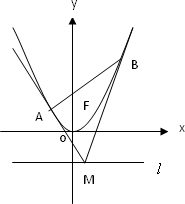
（2013•浙江模拟）如图，已知抛物线的方程为x2=2py（p＞0），过点A（0，-1）作直线与抛物线相交于P，Q两点，点B的坐标为（0，1），连接BP，BQ，设QB，BP与x轴分别相交于M，N两点．如果QB的斜率与PB的斜率的乘积为-3，则∠MBN的大小等于（ ）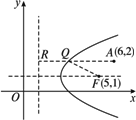
的准线为l，在l上任取一点M，过M作抛物线的切线MA、MB，A、B为切点．
的焦点为
，
是抛物线上横坐标为8且位于
轴上方的点. 
垂直于
轴，垂足为
，
的中点为
（
为坐标原点）. 
的方程；
，垂足为
，求点
是
与圆