题目内容
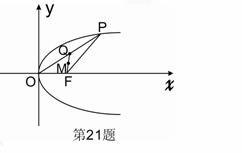
如图,已知抛物线的焦点为F(5,1),准线方程为x=1.
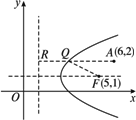
(1)求抛物线方程;
(2)求焦点到顶点的距离;
(3)求顶点坐标.
答案:
解析:
解析:
解:(1)该抛物线方程不是标准形式,应根据抛物线定义求它的方程.
设抛物线上任意一点M(x,y),
据定义,可得![]() =|x-1|,
=|x-1|,
整理,可得(y-1)2=8(x-3).
这就是所求的抛物线方程.
(2)据抛物线几何特征,抛物线焦点到顶点的距离应是焦点到准线距离的一半,而焦点到准线的距离为5-1=4,故焦点到顶点的距离为2.
(3)根据几何特征.顶点是F到准线的垂线段的中点,∴顶点坐标为(3,1).
解析:根据抛物线的定义求解方程,并根据几何性质求解(2)、(3)两问.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 的焦点为F
的焦点为F 过点
过点 的直线交抛物线于A
的直线交抛物线于A ,B
,B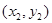 两点,直线AF,BF分别与抛物线交于点M,N
两点,直线AF,BF分别与抛物线交于点M,N 
 的值;
的值; ,直线AB的斜率为
,直线AB的斜率为 证明:
证明: 为定值
为定值
 的焦点为
的焦点为 ,过焦点
,过焦点 轴的动直线
轴的动直线 交抛物线于
交抛物线于 ,
, 两点,抛物线在
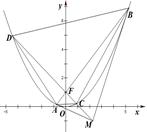
两点,抛物线在 .
.
 交该抛物线于
交该抛物线于 ,
, 两点,求四边形
两点,求四边形 面积的最小值.
面积的最小值. 的焦点为
的焦点为 .过点
.过点 的直线交抛物线于
的直线交抛物线于 ,
, 两点,直线
两点,直线 ,
, 分别与抛物线交于点
分别与抛物线交于点 ,
, .
.
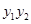 的值;
的值; 的斜率为
的斜率为 ,直线
,直线 的斜率为
的斜率为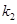 .证明:
.证明: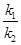 为定值.
为定值. 的焦点为
的焦点为 ,
, 是抛物线上横坐标为8且位于
是抛物线上横坐标为8且位于 轴上方的点.
轴上方的点.  垂直于
垂直于 轴,垂足为
轴,垂足为 ,
, 的中点为
的中点为 (
( 为坐标原点).
为坐标原点).  的方程;
的方程; ,垂足为
,垂足为 ,求点
,求点 是
是 与圆
与圆