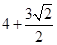题目内容
(本小题共13分)已知圆 过两点
过两点 (1,-1),
(1,-1), (-1,1),且圆心
(-1,1),且圆心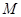 在
在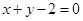 上.
上.
(1)求圆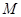 的方程;
的方程;
(2)设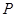 是直线
是直线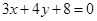 上的动点,
上的动点,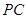 、
、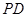 是圆
是圆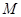 的两条切线,
的两条切线, 、
、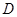 为切点,求四边形
为切点,求四边形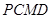 面积的最小值.
面积的最小值.
 过两点
过两点 (1,-1),
(1,-1),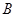 (-1,1),且圆心
(-1,1),且圆心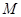 在
在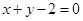 上.
上.(1)求圆
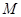 的方程;
的方程;(2)设
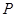 是直线
是直线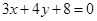 上的动点,
上的动点,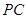 、
、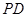 是圆
是圆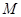 的两条切线,
的两条切线, 、
、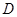 为切点,求四边形
为切点,求四边形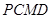 面积的最小值.
面积的最小值.(1)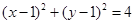 (2)
(2)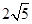
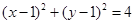 (2)
(2)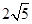
试题分析:(1)法一:
线段
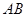 的中点为(0,0),其垂直平分线方程为
的中点为(0,0),其垂直平分线方程为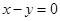 . …2分
. …2分解方程组
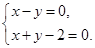 所以圆
所以圆 的圆心坐标为(1,1). …4分
的圆心坐标为(1,1). …4分故所求圆
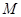 的方程为:
的方程为: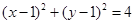 . …6分
. …6分法二:设圆
 的方程为:
的方程为: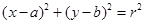 ,
,根据题意得
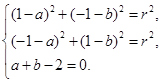 …2分
…2分解得
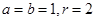 . …4分
. …4分故所求圆
 的方程为:
的方程为: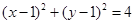 . …6分
. …6分(2)由题知,四边形
 的面积为
的面积为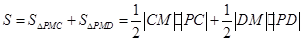 . …8分
. …8分又
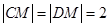 ,
, ,
,所以
 ,而
,而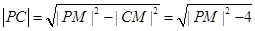 , …10分
, …10分即
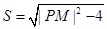 . …11分
. …11分因此要求
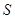 的最小值,只需求
的最小值,只需求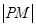 的最小值即可,
的最小值即可,即在直线
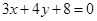 上找一点
上找一点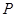 ,使得
,使得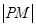 的值最小,
的值最小,所以
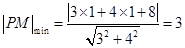 , …12分
, …12分所以四边形
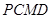 面积的最小值为
面积的最小值为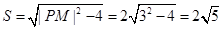 . …13分
. …13分点评:求解直线与圆的位置关系时,要注意数形结合,可以简化运算,还要注意适当转化.直线和圆所涉及到的知识是整个解析几何的基础,并渗透到解析几何的各个部分,但一般难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是圆
是圆 上的动点.
上的动点. 的距离的最小值;
的距离的最小值; 与圆
与圆 相切,且
相切,且 两点,求
两点,求 的面积最小时直线
的面积最小时直线 与圆
与圆 相交于A、B两点,且弦AB的长为2
相交于A、B两点,且弦AB的长为2 ,则
,则 =________.
=________. ,△ABC内接于此圆,A点的坐标(3,4),O为坐标原点.
,△ABC内接于此圆,A点的坐标(3,4),O为坐标原点. ,2),求BC中点D的坐标及直线BC的方程;
,2),求BC中点D的坐标及直线BC的方程;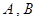 是圆
是圆 上的两点,且
上的两点,且 ,
, ,
,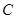 为
为 的中点,连接
的中点,连接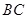 并延长交圆
并延长交圆 ,则
,则 .
. 
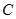 :
: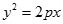 的焦点为圆
的焦点为圆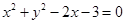 的圆心,直线
的圆心,直线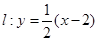 与
与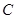 交于不同的两点
交于不同的两点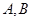 .
.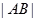 。
。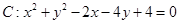 的圆心到直线
的圆心到直线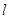 :
: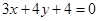 的距离
的距离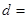
 上的点到直线
上的点到直线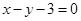 的距离的最大值是( )
的距离的最大值是( )