题目内容
(10分)一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1、2、3、4。现从盒子中随机抽取卡片.
(I)若一次抽取3张卡片,求3张卡片上数字之和大于7的概率;
(II)若第一次抽1张卡片,放回后再抽取1张卡片,求两次抽取中至少一次抽到数字3的概率.
(Ⅰ)P(A)=0.5;(Ⅱ)P(B)= 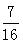 。
。
解析试题分析:(Ⅰ)由题意知本题是一个古典概型,
设A表示事件“抽取3张卡片上的数字之和大于7”, ……1分
∵任取三张卡片,三张卡片上的数字全部可能的结果是{(1、2、3),(1、2、4),(1、3、4),(2、3、4)}共4个, ……3分
其中数字之和大于7的是(1、3、4),(2、3、4),∴P(A)=0.5 ……5分
(Ⅱ)设B表示事件“至少一次抽到3”, ……6分
∵每次抽1张,连续抽取两张全部可能的基本结果有:
(1、1)(1、2)(1、3)(1、4)(2、1)(2、2)(2、3)(2、4)(3、1)(3、2)(3、3)(3、4)(4、1)(4、2)(4、3)(4、4),共16个. ……8分
事件B包含的基本结果有(1、3)(2、3)(3、1)(3、2)(3、3)(3、4)(4、3),共7个基本结果.∴所求事件的概率为P(B)= 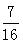 ……10分
……10分
考点:本题主要考查古典概型的概率计算。
点评:中档题,古典概型概率的计算,关键是明确基本事件总数及导致事件发生的基本事件数,此类问题,可借助于“树图法”不重不漏地写出各个基本事件。

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 (
(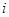 =1,2)表示方案
=1,2)表示方案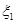 、
、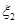 的分布列;
的分布列; 在R上不存在极值点的概率;
在R上不存在极值点的概率;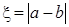 ,求
,求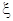 的分布列和数学期望.
的分布列和数学期望.
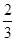 ,乙能攻克的概率为
,乙能攻克的概率为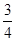 ,丙能攻克的概率为
,丙能攻克的概率为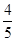 .
.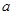 万元。奖励规则如下:若只有1人攻克,则此人获得全部奖金
万元。奖励规则如下:若只有1人攻克,则此人获得全部奖金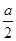 万元;若三人均攻克,则奖金奖给此三人,每人各得
万元;若三人均攻克,则奖金奖给此三人,每人各得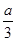 万元。设甲得到的奖金数为X,求X的分布列和数学期望。(本题满分12分)
万元。设甲得到的奖金数为X,求X的分布列和数学期望。(本题满分12分) 的七个大小相同的小球,现从口袋中一次随机抽取两球,每个球被抽到的概率是相等的,用符号(
的七个大小相同的小球,现从口袋中一次随机抽取两球,每个球被抽到的概率是相等的,用符号( )表示事件“抽到的两球的编号分别为
)表示事件“抽到的两球的编号分别为 ”。
”。 且小于
且小于 的概率。
的概率。