题目内容
如图是函数y=Asin（ωx+φ） （ A＞0，ω＞0，|φ|＜π）的图象的一段，求其解析式．
解：由图象可知振幅A=
，…（2分）
又∵周期T=2×（
）=π，∴ω═2，…（6分）
此时函数解析式为y=sin（2x+φ）．
函数经过（
，0），∴2×+φ=kπ （k∈Z），…（8分）
∵|φ|＜π
∴φ=-
…（10分）
∴所求函数的解析式为y=sin（2x-）…（12分）
分析：由图象可知振幅，求出周期，然后求出ω，通过函数经过的特殊点，求出φ，可得函数解析式．
点评：本题考查三角函数的图象求解函数的解析式，注意函数的图象的特殊点的应用，考查学生的视图用图能力．
，…（2分）又∵周期T=2×（
）=π，∴ω═2，…（6分）此时函数解析式为y=
sin（2x+φ）．函数经过（
，0），∴2×+φ=kπ （k∈Z），…（8分）∵|φ|＜π
∴φ=-
…（10分）∴所求函数的解析式为y=
sin（2x-）…（12分）分析：由图象可知振幅，求出周期，然后求出ω，通过函数经过的特殊点，求出φ，可得函数解析式．
点评：本题考查三角函数的图象求解函数的解析式，注意函数的图象的特殊点的应用，考查学生的视图用图能力．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
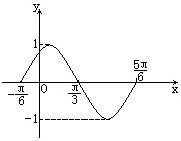如图是函数y=Asin（ωx+φ）（A＜0，ω＞0，|φ|≤| π |
| 2 |
A、向左平移
| ||||
B、向左平移
| ||||
C、向左平移
| ||||
D、向左平移
|
如图是函数y=Asin（ωx+φ）+2的图象的一部分，它的振幅、周期、初相各是（ ）A、A=3，T=
| ||||
B、A=1，T=
| ||||
C、A=1，T=
| ||||
D、A=1，T=
|
如图是函数y=Asin（wx+φ）一个周期内的图象，试确定函数的解析式．
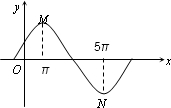如图是函数y=Asin（ωx+φ）(A＞0，ω＞0，|φ|＜| π |
| 2 |
| OM |
| ON |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图是函数y=Asin（ωx+φ）