题目内容
将一个正三角形的各边都n等分,过各分点作其它两边的平行线,一共可产生多少个三角形(包括原来的三角形在内)?
解析:如图,不妨设正△ABC的边长为n,首先考虑“头朝上”的三角形,即平行于水平线的那条边在其对角顶点下方的三角形.
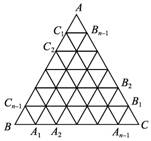
边长为1的“头朝上”的三角形有
1+2+…+n=![]() 个.
个.
边长为2的“头朝上”的三角形有
1+2+…+(n-1)=![]() 个.
个.
……
边长为n的“头朝上”的三角形只有1个.
从而,“头朝上”的三角形共有
![]() 个.
个.
然后考虑“头朝下”的三角形,即平行于水平线的那条边在其对角顶点上方的三角形.
边长为1的“头朝下”的三角形有
1+2+…+(n-1)= ![]() 个.
个.
边长为2的“头朝下”的三角形有
1+2+…+(n-3)=![]() 个.
个.
边长为m的“头朝下”的三角形有
![]() =1k个(n+1>
=1k个(n+1>
故当n为奇数时,“头朝下”的三角形有
![]() .
.
=![]() 个.
个.
当n为偶数时,“头朝下”的三角形有
![]()
=![]() 个.
个.
综上所述,一共产生的三角形的个数为
N=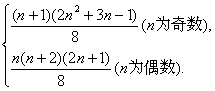

练习册系列答案
相关题目